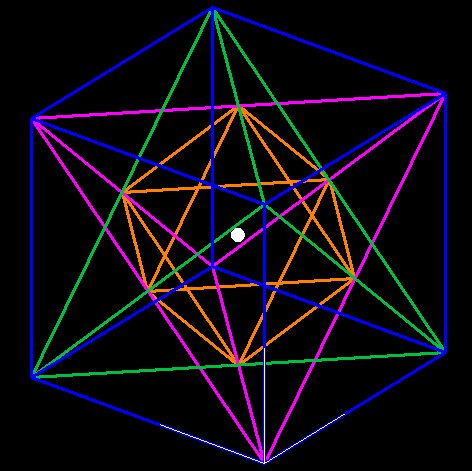
Figure 1. The Star Tetrahedron in the Cube. The white dot is the
centroid.
Figure 1 shows the cube in blue, and two interlocking tetrahedrons, one
in purple, the other in green.
The intersection of the two tetrahedrons forms an octahedron, in orange.
To visualize this, consider that the green tetra comes out of the page
at the top front corner ofthe cube and the purple tetra goes back
toward the bottom corner of the cube, into the page.
This diagram shows the precise relationship of the first 3 Platonic
Solids which are
\/¯2 and
\/¯3 geometry.
What is the volume of a set of two interlocking
tetrahedrons? (star tetra)
What is the percentage volume occupied by a star tetrahedron inside a
cube?
The intersection of the two tetras forms an octahedron.
There are 8 smaller tetrahedron that stick out from the octahedron.
The volume of the star tetra is then the volume of the octahedron + 8 *
volume of each small tetra.
Let side of the cube = 1. Then V (cube) = 1 ^ 3 = 1.
Then edges of the interlocking tetras are all
\/¯2, because each of them is a diagonal of a face of the cube.
Sides of small tetras are exactly 1/2 side of the large tetra, because
each of the large tetrahedrons precisely bisects the other. That is the
magic of the Platonic Solids!
So the sides of the small tetra =
\/¯2 / 2.
We know from The 5 Regular Solids
that the volume of an Octahedron is, (2 /
3 \/¯2) * s^3, so
V(octa) = 2 / 3 \/¯2 * (
\/¯2 / 2) ^3 = 2 / 3
\/¯2 * \/¯2 / 4 = 1/ 6.
We know from The 5
Regular Solids that the volume of a Tetrahedron is,
(1 / 6 \/¯2) * s^3, so
V(small tetra) = 1 / 6 \/¯2
* (
\/¯2 / 2) ^ 3 = 1 / 6 \/¯2
* \/¯2 / 4 = 1 / 24.
V(total small tetras) = 8 * (1 / 24) = 1 / 3.
V(total, star tetra) = 1 / 6 + 1 / 3 = 2 / 6 + 1 /
6 = 1 / 2.
Even though the volume of each large tetrahedron is exactly 1 / 3
of
the cube, the star tetra only occupies one half the volume of the cube!
Below we see the relationship between \/¯2
&
\/¯3 geometry and
\/¯5 geometry.
The dodecahedron is the key, for it contains the cube, as
shown below:
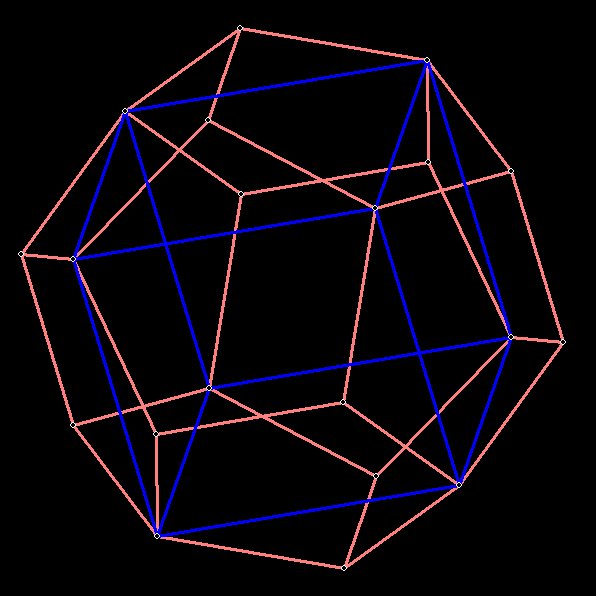
Figure 2 The cube inside the dodecahedron..
The Icosahedron does not contain any of the other Platonic Solids. It
is, itself, a perfect combination of
\/¯2,
\/¯3, and
\/¯5 geometry, for, as we have seen previously, it's faces are
composed of equilateral triangles and the solid itself is composed of
pentagonal caps. The dodecahedron and the icosahedron can morph easily
from one to the other, for they are geometric duals.
For more information, see Icosahedron.
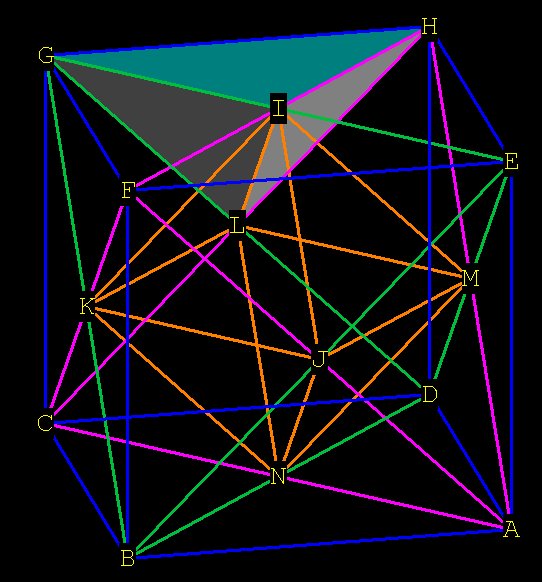
Figure 3. There are 8 congruent solids (GHIL) representing the left
over space in the cube not included in the star tetrahedron volume.
Since the left over space in the cube = 1/2 ,
V(left over solid) = 1/8 * 1/2 = 1 /16 .
These solids have 4 vertices, 4 faces, and 6 edges, thus fulfilling the
Euler requirement that
Faces + Vertices = Edges + 2.
Star Tetrahedron in the
Sphere
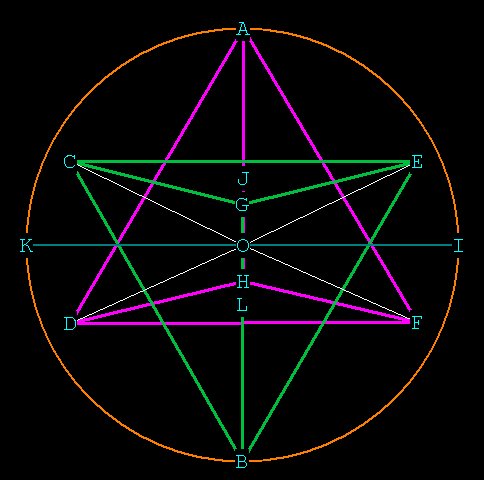
Figure 4. All 8 points of the star tetrahedron touch the surface of the
sphere. In this drawing, G comes out of the page and H goes into the
page.
There are 4 axes of rotation for the star tetra, AB, CF, DE, and GH.
This is seen more clearly in Figure 3.
In Figure 4, notice the planes CGE in green and HDF in purple.
What is the distance between these planes?
What is the angle between the xy plane at the origin and the
planes CGE and HDF?
It turns out that if you have a model of the star tetra you can easily
see that the distance between the two planes is the height of one of
the smaller tetras from the previous section.
We know that the height of a tetrahedron is (\/¯2
/ \/¯3) * side of tetra = (\/¯2
/ \/¯3) * \/¯2
/ 2 =
1 / \/¯3, which is exactly 1/ 3 of the
diameter of the sphere.

Figure 5.
Therefore OJ = one half of 1
/ \/¯3, or 1 / 2\/¯3.
CJ represents the plane CGE and OK represents the plane DFH.
J is the center of the plane CGE, and
L is the center of the plane DFH. OJ is half the distance JL.
OC is the radius of the sphere.
There are two ways to look at this. OC is the height of the green
tetrahedron, which we can calculate, or it is one half of the
cube diagonal CE in Figure 3. There are 4 diagonals, CE, GA, BH, DF.
From Cube we know this distance is
\/¯3 when the side of the cube is 1.
Therefore OC is one half that, or \/¯3 / 2.
Now we have OJ and OC and can get the angle COJ:
cos(<COJ) = OJ / OC = 1 / 2\/¯3
/ \/¯3 / 2 = 1 / 6, so
<COJ = 70.52877937° and
<COK = 19.47122063°.
Special characters:
\/¯ ° ¹ ² ³ × ½
¼
Ø \/¯(ز + 1)




