The Phi Ratio
The Phi Ratio is a proportion. A proportion is a relationship between one quantity and another quantity. It is often very helpful to have something to compare a thing to, in order to establish familiarity with it. For instance, to say "that building is 100" really doesn't help us at all. But if we say "the building is 100 stories" we can get an idea in our minds how large it is. By associating a metric, or measurement, to a number we give it meaning and make it real.
In geometry, comparing 2 quantities to each other helps us establish a relationship between the two quantities. A pure number has no reality, because there is nothing to compare that number to. In geometry, if we can start with a known quantity or length, and then compare every other element in the drawing to that known quantity, we can stay clear on how everything in the drawing relates to everything else.
The Phi Ratio has been known for millennia. It has also been referred to as the Golden Ratio. Euclid called it "Division in Mean and Extreme Ratio." I sometimes shorten this to EMR.
The division into mean and extreme ratio is extremely important because in such a division, there is perfection. The division of any line into EMR, for example, can be continued infinitely small or infinitely large without the slightest error, or “round off” of any kind. So division in EMR or Phi Ratio leads to perfect harmonious growth.
The Phi ratio comes from the division of a line segment such that "The smaller is to the larger as the larger is to the whole."
Consider the line segment GX’, divided at O into line segments GO with smaller length a, and OX’, with larger length b.
Mathematically stated, the above statement becomes .
Let b = OX’ = 1.
.
a² + a = 1 is a second degree polynomial, and you can solve it easily on your
calculator. Just press the "poly" key and enter 1,1,-1.
The calculator will show 2 solutions, the first is
0.618033989 = .
The second is
-1.618033989 = .
Since a is shorter than b, and a is a positive length, a must be . Then a + b = 1 + = .
Notice also that the ratio b/a =
Although is a number it is more properly stated as a
geometric ratio of two numbers. A
ratio is a relationship between two things. When we investigate the
construction of the pentagon, we’ll see that the Phi ratio is stated
mathematically as ,
and that is stated mathematically as .
This might seem uninformative at first, but there is a very understandable and
intuitively sensible geometric interpretation of these quantities that you’ll
be able to easily grasp.
Let’s look at the Phi Ratio in action
The Golden Triangle
The golden triangle is a phi ratio triangle:
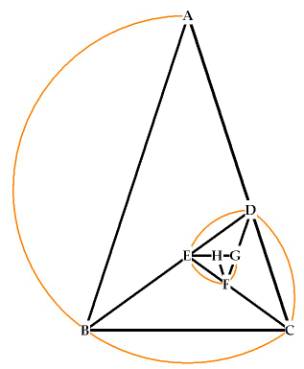
Figure 1 The Golden Triangle
Triangle ABC is a golden triangle because when either of the long sides (AB or AC) is divided by the short side (BC), the result is Phi ( ).
You can see how the triangle divides into itself, always making a triangle with sides and angles in the same proportion. For example, the triangle BCD is also a golden triangle. Triangles CDE, DEF, and EFG are as well, all having the property that the long side of each triangle divided by the short side = . These triangles are made by simply dividing one of the long sides in Phi ratio, and connecting to an opposite vertex. We’ll see how to do that shortly.
In the large triangle ABC, for example, if the line segments AB and BC were
combined to form 1 line, that line would be divided in Phi ratio at B:
Figure 2 The line ABC divided in Phi
Ratio at B.
We can use this idea to easily construct our golden triangles: Take the smaller segment of triangle ABC, BC, and transfer that length to the line AC. Do this by pinning the compass at B with length BC to get the distance, then pinning it again at A and marking off the point D. Now AC has been divided in Phi ratio at the point D! Connect BD with the straight-edge. A second triangle has been now formed, DBC, which is itself a golden mean triangle. The process is absurdly simple, for once a Golden Triangle is constructed, it can be subdivided or grown with hardly any thought whatsoever!
Now refer to Figure 1.
If we let AB = AC = 1, then
BC = BD = AD = .
DC = ,
because + = 1.
Now do the same thing with triangle BCD. Take the short side CD, and transfer
that distance onto BD to find the point E. Then connect CE with the
straight-edge. Another golden mean rectangle is formed, CDE. Continue in this
fashion to subdivide the larger segment of each triangle by the smaller.
You can see that this process can occur indefinitely. The process can be
reversed to make the object larger, on to infinity. The only reason this works
is that the division into Phi ratio occurs absolutely perfectly, with not even
the tiniest error. (Of course there is always construction error, but
mathematically the Phi ratio is perfect division).
Data:
BC = BD = AD = .
CD = CE = BE = .
DE = DF = CF = .
EF = EG = DG = ,
etc.
A little trigonometry reveals that a golden triangle has angles 36-72-72.
Notice the spiral that forms around the triangles. This is called a logarithmic
spiral. If you observe nature, you will
find that she does not use straight lines, she uses curves.
The Golden Rectangle
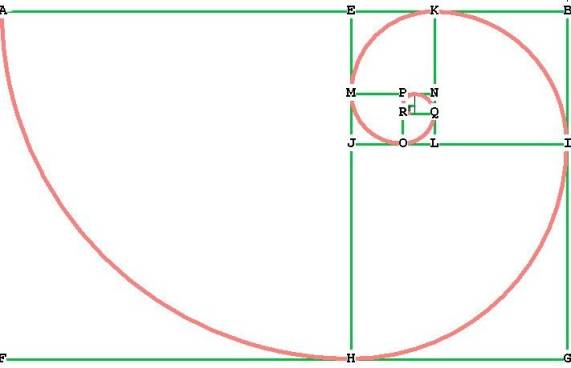
The long sides of the rectangle ABGF (AB and FG) have first been divided into Phi ratio at E and H;
meaning that, for example, the ratio FG / FH = ,
and the ratio FH / GH = .
Remember that Phi is a ratio describing the relationship between two
quantities!
To make the smaller golden rectangle EBGH inside ABGF, simply pin your compass
at F and mark out the distance to A. Then transfer that distance to the point
E, and draw a perpendicular to the point H. Now EBGH is another golden
rectangle. Do the same to make golden rectangle EBIJ, and so on. Notice that
AEHF is a square, and so is JIGH, and so on. This process can go on downward or
upward indefinitely. Again, it is really simple and painless. Once you get the
hang of it, perfect growth or division can occur almost automatically.
Notice that the spiral hits all of the points where a line has been divided
into Phi ratio: H, where FG has been divided into Phi ratio, I, where GB has
been divided into Phi ratio, etc.
What have we learned? That the division into Phi ratio leads to absolutely perfect, harmonious growth. Unfortunately, perfection has no beginning or ending. In other words, we could make our rectangles smaller and smaller, and they would begin to converge at a particular point, but never reach it. As you can see from the above diagram, the spiral keeps circling round and round, never quite reaching the center, or growing outward without end. When nature builds something, she needs a starting and an ending point. Fortunately, hidden within the properties of Phi is the answer.
Next: The Fibonacci Series.
