The Composition of the Pentagon
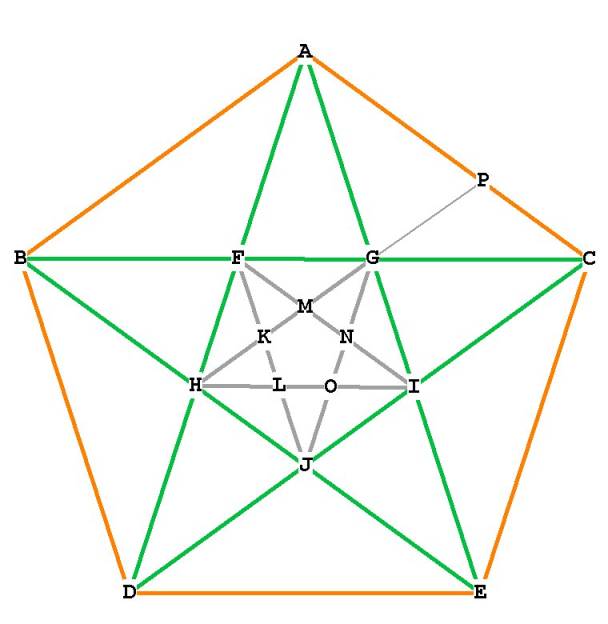
Figure 1
In Figure 1, we have connected the diagonals of the pentagon (in green). These diagonals form another pentagon, GFHIJ, which is rotated 36 degrees from the original. By connecting the diagonals of GFHIJ, we form another pentagon , KLONM, which is rotated 36 degrees from GFHIJ.
The sides of the pentagon are of length 1.
BC = AD = AE = CD = BE
=
AB = BC = CD = DE = EA
=
1 (the sides of the pentagon)
BF = GC =BH = JE =AF = HD = DJ = IC = AG = IE
=
FG = FH = HJ = JI = GI
=
FK = FM = GM = GN = IN = IO = JO = JL = HL = HK =
OL = LK = KM = MN = NO =
...
etc.
Every one of the diagonals of the pentagon divides the other diagonals in Mean and Extreme (Phi) ratio!
Because the sides and the diagonals of the pentagon are in Phi relationship,
every one of the triangles within the pentagon is a Phi ratio triangle. The
number of these triangles is too numerous to mention, but they are all either
36–36–108 triangles (like AFB and GIJ) or 36–72–72 triangles (like DAE, HBF and
GEC).
This is easily seen if you remember that the exterior angles of the pentagon
(as BAC) are all 108 ,
and the diagonals (as AD and AE) trisect
the angle BAC, making the angles BAF, FAG, and GAC all 36
Notice that when the short side of any of these triangles is transferred to a
longer side and a point marked, the resulting two triangles are both Phi ratio
triangles. For example, observe triangle AGC in Figure 1. AGC is a 36–36–108
triangle. When the distance AG is transferred with the compass to line AC at P,
two triangles are formed: AGP, a 72–72–36 triangle, and PGC, a 36–36–108
triangle.
If the small pentagon in the center had its diagonals drawn they too
would divide themselves in Phi ratio and so the process would continue. Smaller
and smaller pentagons would be formed, each one rotating 36 degrees and having
sides times smaller than the previous one.
Where does this end? or begin? The answer is it doesn't!
The pentagon 'ratchets' downward into infinite smallness, and similarly
ratchets upward, getting larger and larger. This can only occur because
division of each line segment is absolutely perfect. Not almost perfect, but
totally perfect. There is never any 'round-off' error.
Notice also that each large triangle (ADE for example) is a golden triangle.
The smaller triangles (AFG for example) are also golden mean triangles.
The pentagon itself can be considered to be a rotating golden mean triangle. If you look at triangle ADE you can see how it rotates 5 times around the center of the circle (O), each rotation being 72 degrees (5 * 72 = 360 for the full circle).
Imagine the pentagon rotating downwards, out of the page, becoming
infinitely small. Envision it rotating upwards out of the page, becoming
infinitely large. The vertices, as they rotate, form a spiral.
So the growth cycle of the pentagon is like this:
On to The Icosahedron
