Construction of the Pentagon, Part II
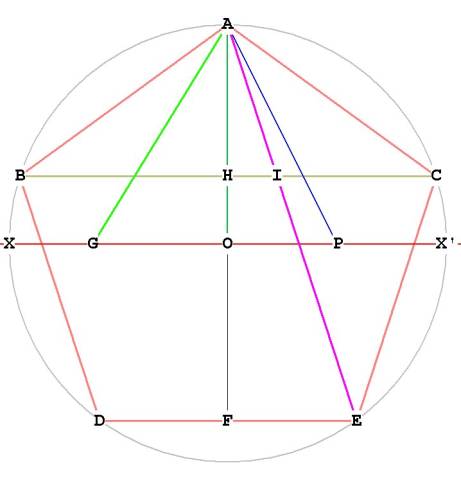
Figure 1
Something very important happens during the construction of the pentagon: the
triangle AOG.
AO = OX' = 1, which is the radius.
We bisected OX' at P, so OP = PX' = 1/2.
By the Pythagorean Theorem, .
GX' = GP + PX', so
This value is called Phi ( ).
GO = GP - OP, so
This value is the inverse of Phi, or .
In Figure 1, the distance AP (the hypotenuse of triangle AOP**) is transferred to the line XX’ at G, such that AP =
PG. When this occurs, the line GOX’ has been divided into Phi ratio at O.
Euclid called this the division into Mean and Extreme ratio.
The larger segment of GX' is OX', the smaller segment is GO.
GX' =
= 1.618033989...
GO =
= 0.618033989...
The triangle AOG has it's larger side (OA)= 1 and its smaller side (OG) = .
Triangle AOG is a Phi right triangle.***
The hypotenuse of triangle AOG, AG, is the result of the division of GOA
into the Phi ratio.
What is AG? By the Pythagorean theorem,
AG² = OA² + OG² =
AG = .
AG = AB, the side of the pentagon. This is the secret to the
design of the pentagon -- its sides are a result of a Phi ratio triangle. In
the next section we will draw diagonals within the pentagon, and we will see
that every single one of them intersects the others in phi ratio, forming
smaller and smaller pentagons within each other, and forming many phi ratio
triangles. The intersection of diagonals AE and BC, for example, divide each
other in Phi ratio at I, and form the Phi ratio triangle AIC. ABC is also a phi
ratio triangle, as is triangle ACE!
What is the relationship between the radius of the circle enclosing the pentagon, and the side of the pentagon?
We know that AB = side of pentagon(s) = * radius.
OA = OB = OC = OD = OE = radius.
so .
What is the height of the pentagon AF?
What is AH? AH bisects BC, a diagonal of the pentagon. We know that the
diagonal of a pentagon is * side of the pentagon. Therefore
.
What is OF?
What is FH?
FH = AF – AH =
Note that : FH / AH =
Therefore, the diagonal BC divides the height of the pentagon, AF, in mean
and extreme ratio.
What is the angle BAC?
We know that AC = 1, and that HC = ,
because BC = .
Therefore,
_________________________________________
**Phi occurs geometrically within a 1, ,
triangle, when the short side distance is
transferred to the hypotenuse. That distance divides the long side of the
triangle in Phi ratio, like so:
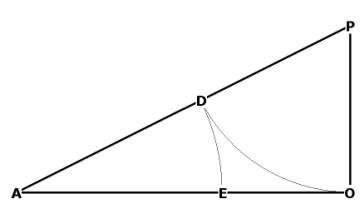
OP is transferred to AP at D, and then AD is transferred to AO at E. AO has been divided in Mean and Extreme Ratio at E. The triangle AOP in Figure 1 is just such a triangle.
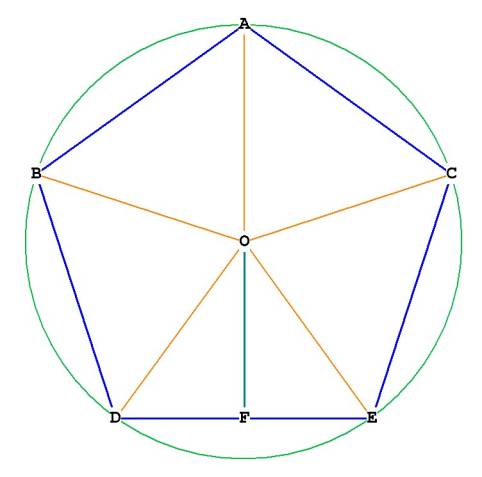
Figure 2
The area of the pentagon is the combined area of the 5 triangles shown in
Figure 1, each of which has a vertex at O.
What is the area of each of these triangles?
Lets work with triangle ODE.
From above we know that the height of triangle ODE, OF, is .
The area of each triangle = 1/2 * base * height:
Area of pentagon = 5 * area of each triangle.
.
On to Composition of the Pentagon, where we further examine the interior of the pentagon and its Phi relationships
