The Construction Of The Pentagon

 

In this section we’ll learn how to construct the pentagon with compass and straight–edge. In part II we’ll look at what we’ve done mathematically. Why are we spending so much time on the pentagon? Because it is fundamental  to the construction of both the icosahedron and the dodecahedron.

First, begin with a circle as usual. Pick a point anywhere on the circle, say X, and with the straightedge draw a line through O, the center, until it intersects the circle again at X'. The radius of the circle is OX = OX'. Let this distance be 1.

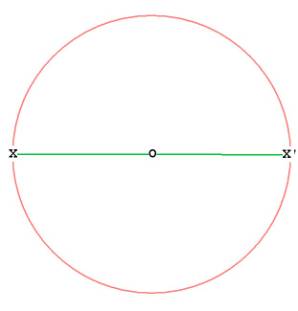
           Figure 1
 

Next, bisect the line XX' with the compass. Pin compass at X, place the other leg at X' and draw an arc from top (above A)  to bottom (below Q).
Pin compass at X', and place the other leg at X. Draw an arc to intersect the arcs you just drew.  I have placed 2 little x's on AQ where both arcs meet. Connect the x's and you have the line AQ in Figure 2:

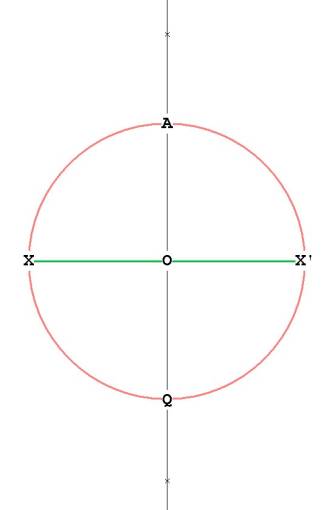
          Figure 2
 

Next, bisect the line OX' at P. We have now divided OX' in half. With the straight-edge connect line AP.

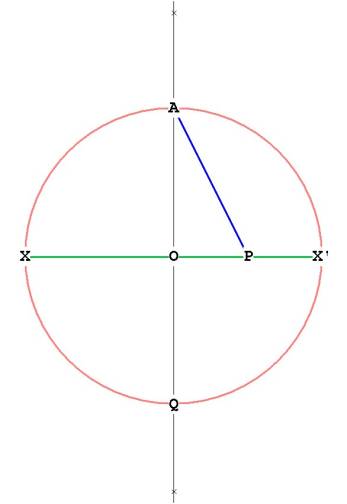
           Figure 3
 
Now take the distance AP and transfer it to  XX'. Do this by pinning the compass at P, with length AP, and drawing an arc down to XX'. Mark that point as G. Now AP = PG and the distance AG (marked in green) is the side of the pentagon. (AG is > AP).
Now, pin the compass at A, with length AG
Draw an arc with the compass from AG through to B, and the other way until it hits the side of the circle at C. Now we have three of the 5 points of the pentagon, A, B, and C.

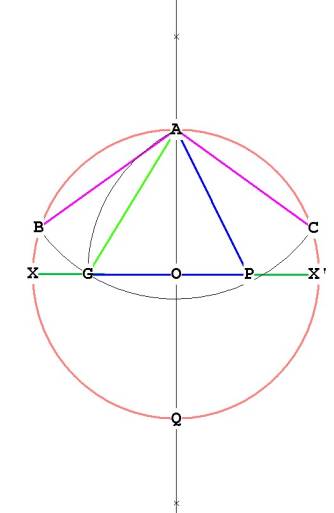
           Figure 4
     

Now, walk the compass around the circle by either pinning it at B or C, with distance AB = AC, and finding D and E. Connect up ABDECA and you have the pentagon.

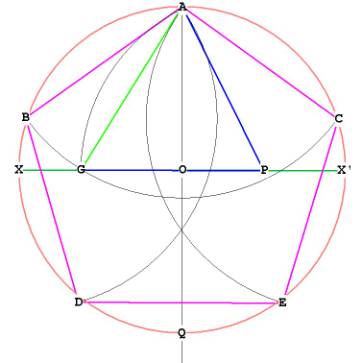
            Figure 5

On to  Construction of the Pentagon, Part II
 

Return to Geometry Home Page     The Big Picture Home