The  Octahedron

 

 

 
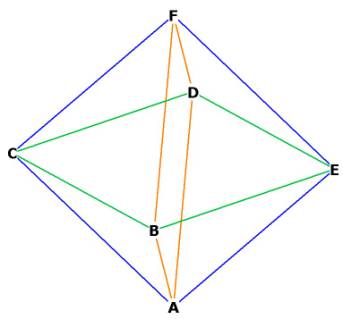
Figure 1  -- showing the 8 faces and 3 squares of the octahedron
The Octahedron has 12 sides, 8 faces and 6 vertices. Count them!

Each of the octahedron's 8 faces is an equilateral triangle, just like the tetrahedron, but the tetrahedron only has 4 faces.

Notice how the octahedron can be considered to be formed from 3 orthogonal squares:
The square BCDE, the square ABFD, and the square ACFE, all 3 of which are planes and all 3 of which are perpendicular to each other.

The octahedron's face angles are all equal because they are all 60°, however, the internal angles of the squares are all 90°. I guess it depends on which way you want to look at it! That's spatial geometry: the position of the observer relative to an object can yield quite different perspectives.

Let's get the volume of the octahedron. All of the octahedron's vertices touch upon the surface of the same sphere that encloses the tetrahedron, so lets put a centroid at O. We will also divide up the face CDF and place a midpoint G in the middle of that face. We place a midpoint H on CD, one of the sides of the octahedron. The side or edge of the octahedron will be hereinafter referred to as ‘os.’

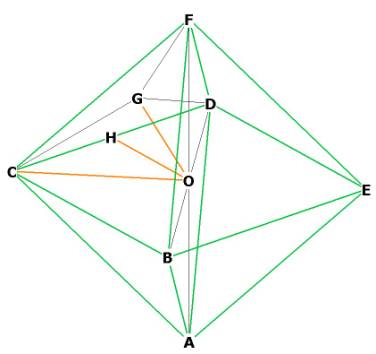
Figure 2
First lets find the volume:
The octahedron consists of 2 pyramids, face-bonded. One pyramid is at A-BCDE, the other at F-BCDE.
The base of each pyramid is the square BCDE. The area of the base is then just os * os = os².
The height of the pyramids are h = OF = OA.
But OF = OA = OC, since the octahedron is composed of 3 squares. FC is just a side of the octahedron.
Therefore we can write: 
 

What is the surface area of the octahedron? It is just the sum of the area of the faces. Since each face is an equilateral triangle, we know from  The Equilateral Triangle  that the area for one face  is   
 

What is the relationship between the radius of the enclosing sphere and the side of the octahedron?
All 6 vertices of the octahedron touch the surface of the sphere. Therefore the diameter of the sphere is just
FA = CE = DB. The radius is 1/2 that, or h, which we found above to be  So,
 

The centroid of the octahedron is at O.
What is the central angle of the octahedron? 90°.
Since the octahedron is made of 3 orthogonal squares, the angle through O from any 2 adjacent vertices must be 90°.   To see this, look at  FOC.

What are the surface angles of the octahedron?  60°, because each of the faces is an equilateral triangle.

What is the dihedral angle of the octahedron?
The dihedral angle is the angle formed by the intersection of 2 planes:

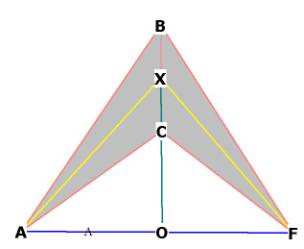
               Figure 3
AXF is the dihedral angle because it is the intersection of the planes ABC and FBC.
ACB and FBC are faces of the octahedron. AX and XD are lines from the face vertex through the mid-face and bisecting an edge of the octahedron, BC.
AF is the diameter of the enclosing sphere, and AO and OF =  r =  h .
OX is just 1/2 of a side of the octahedron BC. You can see this marked in Figure 2 as the line OH.  .
Triangle XOF is right.
 
Dihedral angle = 109.4712206°

 

What is the distance     from the centroid to the midpoint of one of the sides?
What is the distance      from the centroid to the middle of one of the faces?

The distance from the centroid to the midpoint of a side can be seen in  Figure 2 as OH.
We already know this to be .

The distance from the centroid to the middle of a face can be seen in  Figure 2 as OG.
Triangle FGO (see Figure 2) is right, because OG is perpendicular to the face FBC by construction

Figure 4

From  The Equilateral Triangle  we know that .
 
The  distance from the centroid O to the middle of one of the faces =  
What is the distance from the centroid to any vertex?
It is just the radius of the enclosing sphere, or

Octahedron Reference Tables
(included in the book)

Return to Geometry Home Page     The Big Picture Home