The
Icosa–Docedahedron
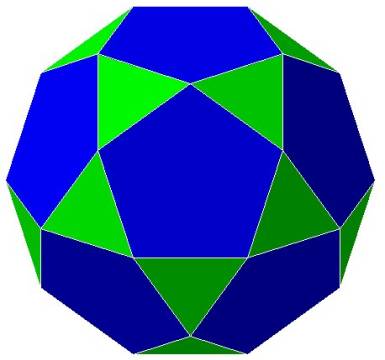
Figure 1 The Icosadodecahedron
This polyhedron is the dual of the rhombic triacontahedron.
It has 30 vertices, 32 faces, and 60 edges.
20 of the faces are equilateral triangles. 12 of the faces are pentagons.
It is probably called the icosa-dodecahedron because in the middle of every
pentagonal face is the vertex of an icosahedron, and in the middle of every
triangular face is the vertex of a dodecahedron.
This polyhedron is composed of 6 'great circle' decagons which traverse the
outside of the polyhedron, sharing the 30 vertices and accounting
for the 60 edges (see Figure 2).
Actually, the rhombic triacontahedron should be called the icosa dodecahedron,
because one icosahedron and one dodecahedron precisely describe its 32
vertices.
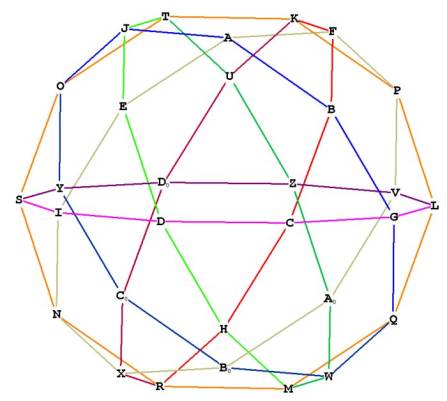
Figure 2 -- showing the icosadodecahedron as composed of 6 interlocking
decagons
The icosadodecahedron (hereinafter referred to as i.d.) has internal planes
within it, as we have seen in other polyhedra. The i.d. has 12 internal pentagons,
2 of which are highlighted, one for each pentagonal face. And of course, the 6
'great circle' decagons:
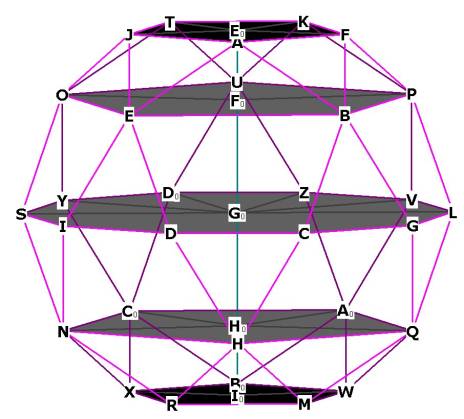
Figure 3 showing 2 of the internal pentagons and 1 internal decagon
Fascinatingly enough, the i.d. also has 5 hexagonal planes! One of these is
highlighted in Figure 4 below.
Notice that the sides of the hexagonal planes are, just like the
pentagonal planes, all diagonals of the pentagonal faces. How can this
be? How can a pentagon and a hexagon both have sides of the same length? We'll
see later on how this happens.
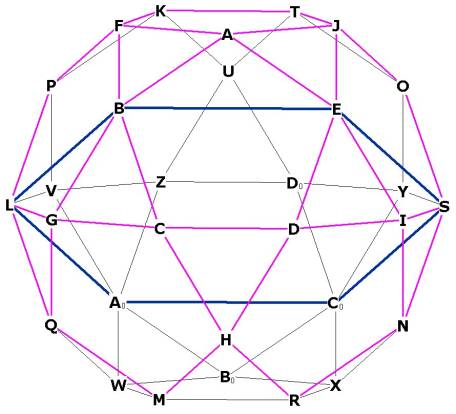
Figure 4 -- showing one of the 5 hexagonal planes of the
icosa-dodecahedron
The i.d. is composed of equilateral triangles internally and externally. The
internal equilateral triangles form from the centroid and any 2 diagonal
vertices of the pentagonal faces.
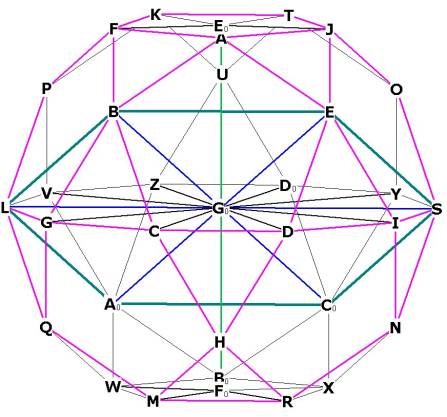
Figure 5 All of these triangles (for example, triangle BGoE) are
equilateral triangles, just like the 20 smaller equilateral triangles of the
faces (for example, BGC). The i.d. has the property that the central angles of
the diagonals of the pentagonal faces (as ![]() BGoE) are 60 degrees.
BGoE) are 60 degrees.
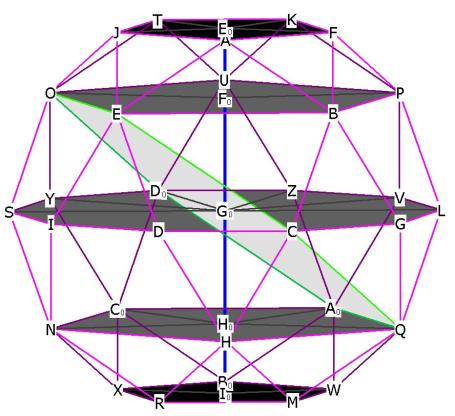
Figure 6 -- showing one of the hexagonal planes in relation to 2 of the pentagonal planes and one of the dodecahedron planes. Now it is clear why the hexagonal plane has the same edge length as the pentagonal planes: the hexagonal plane uses different diagonals of the pentagonal faces, and so is angled relative to the pentagonal planes.
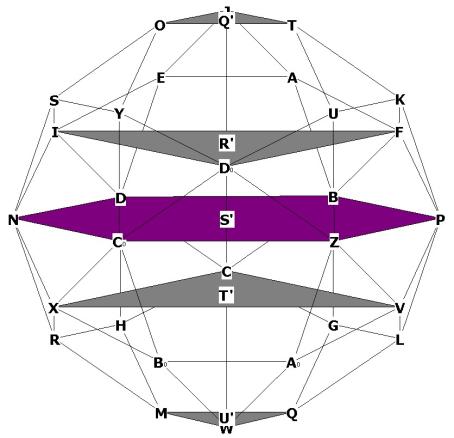
Figure 6A -- showing that the hexagonal plane is parallel to the top and bottom
triangular faces, and also showing the 2 large triangular planes.
What is the volume of the icosadodecahedron?
We will use the pyramid method again. There are 20 triangular pyramids and 12
pentagonal pyramids.
Although the icosa-dodecahedron is a semi-regular polyhedron, all of its
vertices touch on the same sphere. So the radius of the sphere surrounding the
i.d. is the same for each vertex. That makes our calculations a little easier.
In order to make life simpler, it would be nice to know the relationship
between the side and the radius of the i.d. I will present 2 ways of getting
this: the absurdly simple way, and the 'brute force' method.
The simple method is to recognize that the central angle of the i.d. is 36°,
and that every vertex on the i.d. is part of a decagon. Therefore any 2
vertices combined with the centroid forms a
36 -72 -72 isosceles triangle. We recognize this immediately as a Golden
Triangle. The relationship of the short side to any of the long sides of
such a triangle is therefore 1 to ![]() . And so the relationship of the radius to any vertex is r =
. And so the relationship of the radius to any vertex is r = ![]() ids. (ids = icosadodecahedron side).
ids. (ids = icosadodecahedron side).
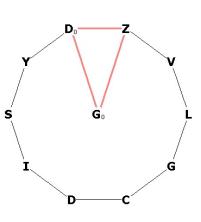
Figure 7 - showing DoGo = GoZ = radius,
and the golden triangle Go-Z-Do
We can show this with the 'brute force' method as follows:
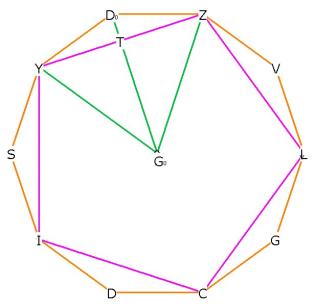
Figure 8 -- deriving the relationship between radius (GoZ) and side (ZDo)
ZY is the side of the pentagon. Go is also the center of the pentagon.
ZT is just one half the side of the pentagon, because GoDo is a bisector of ZY.
We know the distance GoZ, Construction of the
Pentagon Part 2 as
![]() side of pentagon.
side of pentagon.
GoZ is also the radius of the enclosing sphere around the i.d.
We also know from this that GoT = ![]() side of pentagon.
side of pentagon.
Therefore TDo = ![]() -
- ![]() =
= ![]() side of pentagon.
side of pentagon.
What is the relationship between the side of the pentagon and the side of
the decagon?
Let's find ZDo, the side of the decagon, in terms of the side of the pentagon.
ZDo˛ = TDo˛ + TZ˛ =
ZDo = ![]() side of pentagon.
side of pentagon.
But r = ![]() side of
pentagon, so side of pentagon =
side of
pentagon, so side of pentagon = ![]() .
.
.
.
Therefore, ZDo, the side of the decagon and the side of the i.d. =
![]()
Now let’s resume the volume calculation. First we’ll calculate the volume of
a pentagonal pyramid. Refer to Figure 9 below.
From Area of Pentagon we
know area = ![]() ,
,
and the distance mid-face to any vertex of a pentagon,
HoF, = ![]() ids.
ids.
GoF = ![]() *ids. GoF is just the radius of the enclosing sphere
*ids. GoF is just the radius of the enclosing sphere
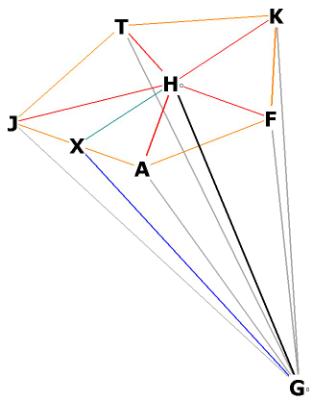
Figure 9 -- one of the 12 pentagonal pyramids of the i.d.
To find the height of the pyramid, take right triangle GoHoF.
h˛ = GoHo˛ = GoF˛ - HoF˛ ![]()
h = ![]()
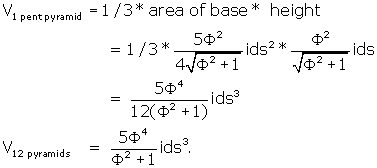
That takes care of the pentagonal pyramids. There are still 20 triangular
pyramids.
Each triangular face area =![]() and the height is as follows:
and the height is as follows:
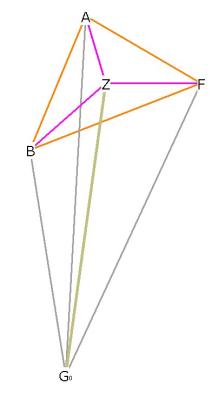
Figure 10 - a triangular pyramid of the icosadodecahedron
Triangle GoZF is right by construction.
GoF = ![]() *ids, being the radius of the enclosing sphere.
*ids, being the radius of the enclosing sphere.
ZF is, from Equilateral Triangle, ![]()
Therefore h˛ = GoZ˛ = GoF˛ - ZF˛ = ![]()
h = ![]()
So ![]() = 1/3 * area of
base * pyramid height =
= 1/3 * area of
base * pyramid height = ![]()
= ![]()
![]()
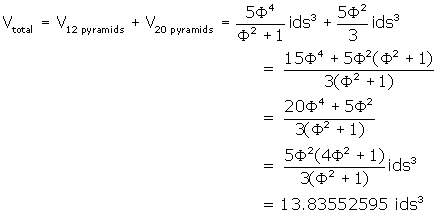
This figure is slightly larger than the volume of the rhombic
triacontahedron. This larger figure is easily explained by the fact that both
the outer radial distance of the r.t., and the radius of the i.d., are ![]() * side. Since ALL vertices of the icosadodecahedron lie on
this sphere, and only 12 of the vertices of the rhombic triacontahedron do, the
volume of the icosadodecahedron is naturally larger.
* side. Since ALL vertices of the icosadodecahedron lie on
this sphere, and only 12 of the vertices of the rhombic triacontahedron do, the
volume of the icosadodecahedron is naturally larger.
What is the surface area of the icosadodecahedron?
It is 12 * area of pentagonal face + 20 * area triangular face =
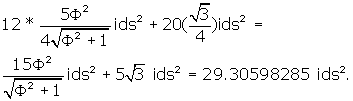
What is the central angle of the icosadodecahedron?
Because all of the vertices of the i.d lie along the 6 'great circle' decagons,
the interior angles are all 360° / 10 = 36°. Notice that each of the
central angles to adjacent vertices forms a Golden Triangle with angles 36°,
72° and 72°.
We saw earlier how the central angle between two diagonal vertices on any of
the pentagonal faces, is 60° and how this forms a hexagon, and thus large
internal equilateral triangles (see Figure 5 and triangles BGoE, LBGo, GoES,
LAoGo, AoGoCo, GoCoS). We were curious as to how the side of the hexagonal
plane could be the same length as the side of the pentagonal plane. If
you look at Figure 6 you can see that the sides of both of these planes are a
diagonal of any of the pentagonal faces. It is clear then, that like the
rhombic triacontahedron and the icosahedron, the icosadodecahedron is based on
the pentagon.
Because the length of the radius (distance from centroid to any vertex) is ![]() * side of i.d., and
the diagonal of any pentagon is also
* side of i.d., and
the diagonal of any pentagon is also
![]() * side of i.d., the hexagonal plane is formed .
* side of i.d., the hexagonal plane is formed .
What are the surface angles of the i.d.?
There are 2 of them. One is the angle forming the triangular faces, equal to
60°, and the other is the angle forming the pentagonal faces, equal to 108°.
What is the dihedral angle of the icosadodeccahedron?
For this calculation, go to IcosaDodecahedron Dihedral Angle .
Let's collect some information we have already calculated:
Distance from centroid to a vertex = radius = ![]() *ids.
*ids.
Distance from centroid to mid-pentagonal face = ![]()
Distance from centroid to mid-triangular face = ![]()
Distance from centroid to mid-edge = ![]()
Or, in decimals,
Distance from centroid to a vertex = radius = 1.618033989 *ids.
Distance from centroid to mid-pentagonal face = 1.376381921 *ids.
Distance from centroid to mid-triangular face = 1.511522629 *ids.
Distance from centroid to mid-edge = 1.538841769 *ids.
Now let's calculate the separation of the various planes in the
icosadodecahedron.
We want to get the distances between Eo, Fo, Go, Io and Ho.
Let's first get EoFo.
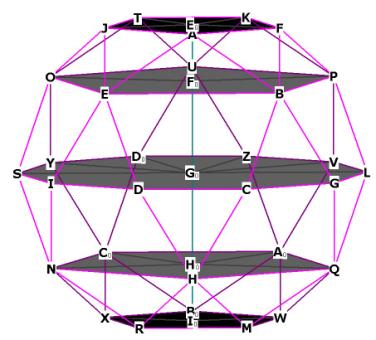
Figure 3, repeated
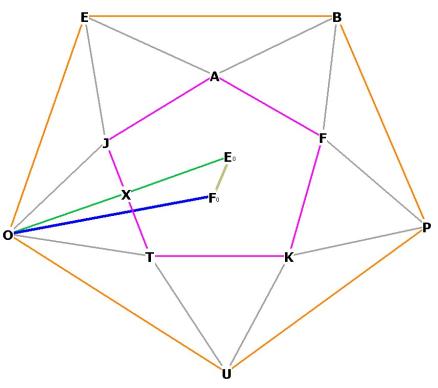
Figure 11a. Top view, refer to Figure 3
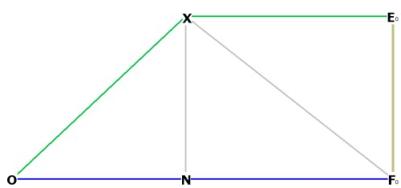
Figure 11b The distance between the first 2 pentagonal planes (EoFo) of
the icosadodecahedron. Note that although OXEo appears to be a straight line in
Figure 11a, it is actually the dihedral angle of the solid.
The top pentagonal plane on the i.d. is the plane AJTFK, in purple in Figure
11a and the top plane in Figure 3. The large pentagonal plane UPBEO is marked
in orange.
The point Eo is the center of the small pentagon, Fo is the center of the large
pentagon.
AJTFK is on top of UPBEO.
The angle FoEoX is right. EoFo is the line perpendicular to the plane AJTFK
from the center of the plane UPBEO, and is part of the diameter of the sphere
which runs through the centroid O.
The angle OFoEo is also right, the line EoFo is perpendicular to the plane
UPBEO.
OX and XEo can be easily calculated.
OX is just the height of an equilateral triangle,![]() , and XEo is the distance, in a pentagon, from the center to
any mid-edge. We know from Construction of the Pentagon Part 2 that this distance is
, and XEo is the distance, in a pentagon, from the center to
any mid-edge. We know from Construction of the Pentagon Part 2 that this distance is ![]()
The distance OFo is just the distance from the center of the large pentagon, to
one of its vertexes. From Construction of the Pentagon Part 2
we know this distance to be
![]() * side of the large
pentagon.
* side of the large
pentagon.
We may draw a perpendicular bisector from X to N on the line OFo.
![]() EoXN and
EoXN and ![]() XNFo are both right.
XNFo are both right.
We now have a rectangle XNFoEo with 4 right angles at the corners, and XN =
EoFo, XEo = NFo.
Now we can find the distance ON, for it is just OFo - NFo.
Then we can work with triangle ONX to find XN and we have EoFO.
First we must find OFo in terms of the side of the icosadodecahedron.
Remember that OFo is ![]() * side of the large
pentagon. But the side of the large pentagon is just the diagonal of any the
pentagonal faces of the i.d.
* side of the large
pentagon. But the side of the large pentagon is just the diagonal of any the
pentagonal faces of the i.d.
Therefore the side of the large pentagon is ![]() * ids.
* ids.
We can then write OFo = ![]()
(Note that this distance is precisely the distance from the centroid to the mid-face of any of the pentagonal faces!)
NFo = XEo = ![]()
Then ON = OFo - NFo = ![]()
= ![]()
From this we gather that ON = NFo.
XN˛ = OX˛ - ON˛ = 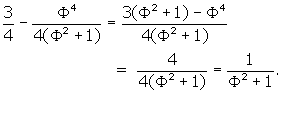
XN = EoFo = ![]()
Therefore the distance between the first two pentagonal planes is ![]()
Now we can easily find FoGo, the distance between the large pentagonal plane
and the plane of the decagon which contains the centroid.
This distance is just EoGo - EoFo.
EoGo is the distance from the centroid to mid-face of pentagon,
which we found above to be ![]()
So FoGo = ![]()
=
![]()
What is the relationship between EoFo, FoGo and EoGo?
EoGo / FoGo = 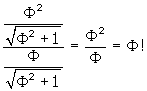
Therefore the radius EoGo is divided in Mean and Extreme Ratio at Fo.
We can make a table of relationships of the distances between the pentagonal
planes. If we let EoFo = 1, then
(Available in the book)
What are the distances between the triangular planes and the hexagonal plane
which runs through the centroid?
(Refer back to Figure 6A above).
We want EoFo.
The large equilateral triangle DoIF in Figure 6A has sides equal to the
distance DoF = FI = DoI in Figure 12:
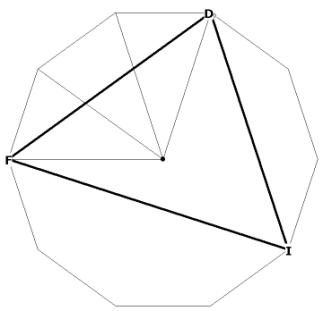
Figure 12 Showing the length of the sides of the large triangular planes
You can see this in Figure 3 by examining the vertices Do,
Y, S, I which are part of one of the 'great circle' decagons. The length of
each side of the triangular plane is DI. The other two legs of this large
equilateral triangle are each part of a different decagon.
From Decagon
we know the edge length of each side of triangle DoIF is ![]() ids. You can see this in Figure 6A by examining the vertices
Do, Y, S, I which are part of one of the 'great circle' decagons. The other two
legs of this large equilateral triangle are also part of a different decagon.
ids. You can see this in Figure 6A by examining the vertices
Do, Y, S, I which are part of one of the 'great circle' decagons. The other two
legs of this large equilateral triangle are also part of a different decagon. 
Figure
6A, repeated
R’ is
the center of the triangular face DoIF. T’ is the center of the triangular face
CXV, and O’ is the centroid. We want to find R’T’, the distance between the two
triangular planes. We will first find O’R’.
The solution is quite simple, actually. The distance DoR’ is known. DoR’ is the distance from the center of an equilateral triangle to an i.d. vertex. O’R is also known. O’R is just the distance from the centroid to a vertex of the i.d. R’ lies directly above O’. Therefore the triangle O’R’Do is right and we may write
![]() .
.
O’Do = ![]() *ids, and from Equilateral Triangle we know
that R’Do =
*ids, and from Equilateral Triangle we know
that R’Do = ![]() .
.
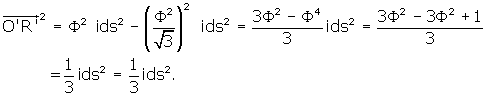
![]()
Because the analysis is precisely the same for O’T’, the
distance O’T’ also equals![]() , and
, and
R’T’ = ![]()
What is the distance Q’R’? This is the distance
between the triangular face OJT and the plane DoIF. The analysis is the same as
above, except that the side of the triangular plane OJT is now ids, instead of ![]() (Why? Because OJT is a face of the i.d.) Therefore
(Why? Because OJT is a face of the i.d.) Therefore 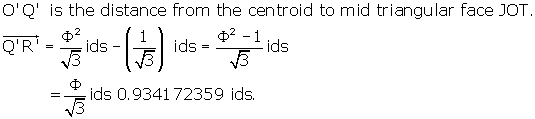
Q’R’ / O’R’ = 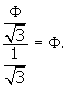
What is the angle any of the hexagonal planes make with the
plane of the decagon?
In Figure 6A the hexagonal plane is highlighted in purple.
This can be seen by observing the plane of the hexagon as it intersects the plane of the decagon in Figure 6.
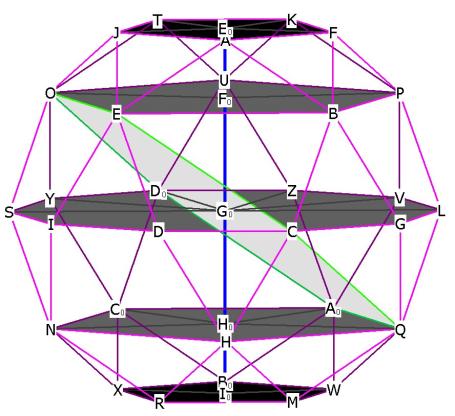
Figure 6, repeated
Notice that ![]() OGoS is the angle of the hexagonal plane as it intersects
with the central decagon, and that is it also a central angle of the i.d. This
angle, of course, is 360 / 10 = 36°.
OGoS is the angle of the hexagonal plane as it intersects
with the central decagon, and that is it also a central angle of the i.d. This
angle, of course, is 360 / 10 = 36°.
Conclusions:
What have we learned about the icosadodecahedron?
Mainly, that it is pentagonally based.
The triangular faces fill in the gaps between the pentagonal faces.
All of the radii form Golden Triangles with any 2 adjacent vertices.
The spacing of the pentagonal and decagonal internal planes are based upon the
division of the space into Mean and Extreme Ratio.
Return to Geometry Home
Page The Big Picture Home
Icosa–
Dodecahedron Reference Chart
(available in the book)
