GEOMETRY FUN
2 Dimensional Geometry
In this essay we’re going to have a little fun
pretending that
we’re the creator of the universe. In essence, we're going to play God.
If you're religious and are offended by this idea then I'm sorry, but
if you're like me, you've sometimes wondered what the world would be
like if you got to make all the decisions. So, in a spirit of good fun,
let's continue.
Let’s say there is nothing in the
universe, because
nothing has been created yet. If nothing existed at all, and there were
no galaxies,
stars, planets, or even atoms, how would we begin the creative process?
Well, even though I'm playing God, I'm really just a dopey human, so
we'll stick with something simple: building some simple 2
dimensional
polygons. (Poly = many, gon = side).
We’ll say
that, like in
dreams, our thoughts can manifest instantly. We’ll also say that we
don’t
know
anything to start off; in other words, our consciousness is like a
newborn baby
and we don’t have any idea of physics or chemistry or what a planet
looks like,
or what atoms and molecules are, because they haven’t been thought up
yet! We’ll
say that each thought we have creates a little point mass, and that we
can
combine them together.
So right now we have a consciousness that is just hanging out, and it's
really boring because there's nothing to do! Nothing to play around
with.
Let’s
call our self-aware consciousness Hal (actually consciousness doesn’t
have gender, but we’ll say
Hal is
a him). Before we get started, we'll leave Hal hanging out in space for
a bit and
look at
a few assumptions; after all, he'll need plenty of time to think about
how he's going to proceed.
If you want you can just skip this part and go right
to Let’s
Get Started below.
Here are the assumptions we’ll be operating under:
1) The fundamental 'particle' or quanta of energy in the universe is
a
thought. Let’s call this a POINT.
2) All matter and energy will be ultimately composed of POINTS.
3) We’ll say that POINT’s are conscious, because they are thoughts, and
since
we are conscious, so are our thoughts. In other words, POINTS are
conscious, because they proceed directly from consciousness.
4) POINT’s can perceive omni-directionally. Meaning, that if you
placed
your awareness in a POINT, you can perceive in all directions.
Euclid defined a POINT as, “That which has no part.” We’re saying here
that a
POINT is not an abstraction, it has consciousness and existence. In
other
words, for our little game, we’ll say a POINT is real.
We will say that a LINE is the connection of awareness between
2
POINTS. It comes about when we create another POINT, or, when two
POINTS become
aware of each other.
A LINE is either curved or straight. If it is perfectly straight then
there is
instant communication, because there is absolutely no change of
direction. So
there is no time between a communication from one end and the receipt
of that
communication at the other. We’ll say there’s no medium, like water, or
air, or
“ether,” to stop our perception. We’ll assume that each POINT has a
sort of
instantaneous telepathy with other POINTS, and with us.
If the LINE is curved then there is a point within the concave boundary
of the
line from which all the other points are generated and to which they
are all
related. The arc of a circle is an example of a curved line. The center
of the
circle is the point to which all of the other points on the
circumference are
related (all the points on the circumference are the same distance from
the
center).
Because curved lines are constantly changing direction, there is
persistence. In
other words, to go in a new direction requires
a decision at every step along the way, a slight
hesitancy which creates time.
A note on central angles: a central angle is the angle a point on the circumference makes with the center of the circle and an adjacent point on the circumference. If you look at the diagrams below, you will see that the central angle is also a measure of the chord length of the polygon (the side of the polygon).
Assertions:
All polygons are inscribed in circles. The circle is the beginning
point for
ALL 2 dimensional geometry.
The circle is Unity.
Growth comes from the division of Unity.
The circle provides the reference point from which geometric order
proceeds. In
other words, all Form is created from Unity.
Let’s Get Started!
To follow along with this discussion, you can get out paper, a straight edge, and a compass.
OK, Hal is hanging out in nothingness (pretend that you are Hal).
There isn’t
even any space yet, just a pure potential who is self-aware. How does
he start
to make anything?
Well, the first thing Hal decides is that it would be cool to have
something outside
of himself to look at. As soon as Hal
decides that, he has just created a POINT! Lets call that POINT A. Hal
has also
created space between himself and A, so he can view it.
In other words, without space, there would be no separation between Hal
and
POINT A. Hal now realizes that POINT A is different from him,
because it
occupies a different point in space. At the same time, he realizes that
POINT A
is his thought, so Hal can identify with A as well. This is a state of
affairs
Hal has never considered before, because prior to the creation of A,
there was
just Hal and nothing else.
A
![]()
O
OA = r
After pondering this for a while, Hal realizes he has a radius, or a
limiting point of perception. Hal is at O and has just created a
LINE OA.
What can he do with that?
Well, right now the only distance Hal knows is r, but he gets the
brilliant
idea of making more and more POINTS the same distance away. And when he
does
that, he is astonished to have created a circle. Hal can see right off
the bat
that once the circle is connected, it really has no beginning or
ending, and it
reminds Hal of himself, for he can never remember a time when he was
not self
aware.
All of the points Hal will create, up to and including length r, will
be his
universe. He can have a whole bunch of POINTs, each of which is
conscious, the
outer boundary of which represents the circumference of the
circle of his
awareness (we are only talking 2 dimensions here). For our purposes we
will
deal only with points on the circumference.
A circle – Hal’s universe.
What’s next?
The only information Hal has is r. He has created a bunch of connected
POINTS
to form a circle, but what can he do with that?
Hal decides to go to A and look through A at his circle. He admires his
circle
and thinks that it is really the most wonderful thing in the universe.
And
since it is the only thing in the universe at this juncture, Hal is
perfectly
correct!
Hal gets the brilliant idea to go to another POINT the same distance r
from A
on his circle, and he calls that POINT B. Hal has no idea what’s going
to
happen with this, but he’s really excited so he looks in the other
direction from
A and moves to another POINT the same distance, r, at C. At C he does
the same
thing to get to D, and at D to create E.
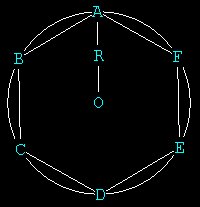
Now Hal realizes something really cool: the 6 points, A,B,C,D,E,F
are all exactly
spaced around
the circumference.
If you are doing this with compass straight-edge and paper, start by
pinning
the compass at A, with length OA, and find the intersection with
the
circumference at B and C. Pin the compass at B and find
another
point of intersection with the circumference at D . Pin the compass at
C and
find another point of intersection at E. From E (or D) find
F.
The hexagon -- the first regular polygon in Hal’s universe. Central
angle
(AOB) 360 / 6 = 60 degrees
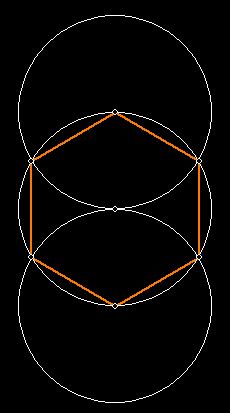
Another way to get the hexagon is pin the compass at A and draw a circle, then pin the compass at D and draw another circle. The intersections of the three circles will form the POINTs of the hexagon:
We have divided the circle into 6 parts and have identified 6 POINTs
and 6 LINEs.
The LINES in the diagram represent the communication between each
conscious
POINT in Hal’s hexagon. Because the POINTS A,B,C,D,E have been
created by
Hal, they have a little bit of Hal’s conscious awareness 'built in' to
them, as
an inherent part of their nature. They can be used by Hal as positions
from
which to view the hexagon from any POINT.
When Hal places his awareness at any POINT he sees the exact same
thing,
because all of the distances are equal around the circumference and to
the
center.
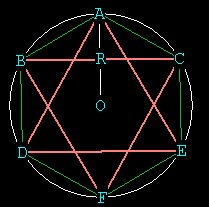
We are now at F. From F with the straight-edge connect
to B and
C. We have now created our second regular polygon, the equilateral
triangle.
The triangle is the minimum polygon, with 3 vertices.
From A connect to D and E. Now we have, inscribed in the circle, 2
interlocking
equilateral triangles. When we look at this figure 3 dimensionally
later, it
will be 2 interlocking tetrahedron's forming the vertices of a cube.
The circumscribed Equilateral Triangle -- the minimum polygon
in our
universe
Central angle (AOE) 360 / 3 = 120
The first regular polygon in creation, then is the hexagon! This
seems
counter intuitive, doesn't it? How could something with 6 vertices come
before
something with 3 vertices? Of course you can stop after the first 3
points A,
B, C and connect them to form a triangle, but this triangle doesn't
have equal
sides. Remember, all we knew going around the circle distance-wise was
r, the
radius!
Hal could have connected immediately to O after making B and
formed an
equilateral triangle, but this would involve him as one of the
vertices.
So in the beginning, there is a circle, and then 6 points on the circle
forming
the hexagon. From the 6, immediately comes the 3.
As we gaze out upon our hexagon and our triangles we realize that the
lines of
communication to all 6 points form 6 smaller equilateral triangles all
with
side lengths equal to r. We realize that the triangle is the simplest
polygon
and that 6 equilateral triangles could form a hexagon. We also can see
that the
intersections of the lines of the equilateral triangles forms another
hexagon
inside, and that this interior hexagon is rotated 30 degrees from the
outer
one.
We are on a roll now. We have now created a regular polygon
with 6
vertices and one with 3. Lets try and see if we can construct one with
4
vertices. After a little thought we figure it out. First
with your
straight-edge connect up points A and F. That's the easy part. We now
have the
'y axis.' To get the 'x axis' we have to figure out how to bisect the
lines BD
and CE.
We still have our compass set to r! Pin it at B and draw and arc above
BD. Pin
it at D and draw an arc to intersect the first one. Do the same
with the
line CE. Now with the straight-edge connect the two points
together,
going through O.
The intersection of this line with the circle comes at H and at I. The
line IH
is called a perpendicular bisector of the line AF, through O. Now IH is
our 'x
axis.'
Bisecting the line xx'---
Pin the compass at x with the other leg at x', and mark an arc above
and
below the circle.
Pin the compass at x' with the other leg at x, and mark an arc above
and below
the circle that intersects with the other arc. Now connect the
line
through O.
Now connect A, I, F, H to form the square. We can see that these points are regularly spaced because the angles between them are equal.
The Square -- Central angle(AOH) = 360
/
4 = 90
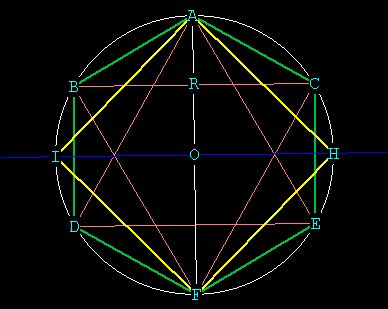
We have created 2 more POINTs I and H and now have 4 polygons, a
hexagon
(green), 2 equilateral triangles, (pink), and a square (yellow). Here
we see
that growth comes from further division into Unity.
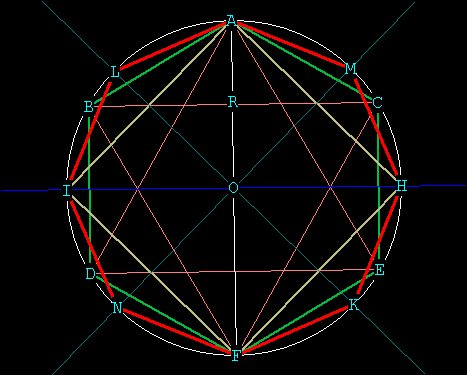
Now that we have our square, we can proceed to the 8 sided polygon, or
octagon.
All we have to do is bisect each one of the sides of the square, which
is the
same thing as bisecting the central angles of the square. We
bisect lines
AI and FH through O, and bisect lines AH and IF through O, to get
points L,M,N,
K
The octagon -- formed from the square (the octagon is in red).
Central angle
(MOH) 360/8 = 45
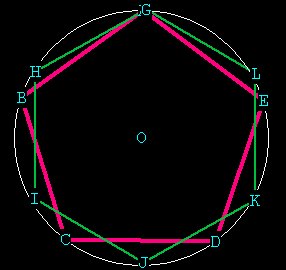
Now lets try for the 5-sided polygon to complete sequence of
3,4,5,6.
This one is a little tricky and requires a lot of thought. See "The
Construction of
the Pentagon" for instructions.
The Pentagon --- representing continuous harmonic growth.
Central
angle (GOE) = 360/5 = 72
From the pentagon we can immediately get the 10-gon, or decagon, by bisecting the sides (and angles) of the pentagon, just like we bisected the sides of the square to get the octagon. It turns out that the sides of the decagon are in Phi ratio to the sides of the pentagon!
The decagon -- formed from the pentagon. Central angle
VOU = 360
/ 10 = 36
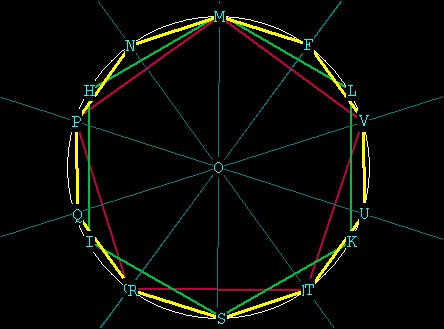
Here we have demonstrated all of the polygons from 3 to 10 that can
be
precisely generated in one and only one circle. There are 2
polygons
which are currently thought to be accurately impossible to draw
geometrically: the 7-gon (heptagon) and the 9-gon (enneagon). The
7-gon
is impossible to construct because the central angles which represent
its edges
are repeating decimals
(i.e. 360 / 7 = 51.428571428571..... this number can't be pinned down).
The 9-gon can't be constructed, even though its central angle is an
integer
(360 / 9 = 40) because it involves the trisection of a 60 degree angle.
Think
about it. We need a 40 central angle. We don't have protractors
with nice
little angles marked off on them, only compass and straight-edge.
So we have to work with an already-defined central angle. We have the
following
angles from the diagrams shown above:
120, 90, 72, 60, 45, 36.
The problem: How to get 40 from any of these?
The only possible way is to trisect either the 120 (120 / 3 = 40) or
trisect the 60 (60 / 3 = 20. 20 + 20 = 40). But with the standard
compass and
straight-edge, we can only bisect!! If you don't believe it is
possible
to trisect an angle, get out your paper, compass and straight-edge and
try it
for yourself!
It turns out we can only construct polygons of 2,4,5,6,8,10,12,15,16,
17,20
sides if we use standard compass and straight-edge. (1)
However, the 7-gon and the 9-gon, in fact ANY polygon can be
constructed
using the new compass developed by James D. Watt called the Z-wheel.
The Z-wheel is attached to the marking leg of a standard compass
and is
used to measure arc lengths.
In footnote (2) below is a picture of Mr. Watt's compass, taken
from his
website, with a brief description.
With this compass any n-gon can be constructed by the multiplication of
radial
distances. In this method, PI is unnecessary. The unit of measure is
simply the
linear, whole number, radial distance which automatically generates a
circumference. The only difficulty with this method is that it
requires, in
particular cases, n concentric circles to produce an n-sided polygon.
But that
doesn't detract from its power.
Of course, some people will say this is cheating, for it is really
impossible
to find and mark an exact point on the z-wheel, but there is also an
error when
pinning a standard compass to any point! The z-wheel is an interesting
idea
because it uses 3 dimensions to solve a puzzle in 2 dimensions. And
anyway, we're just having fun, so we can do whatever we want!
First lets start with the 9-gon, go to the 7-gon and then show and by
that time
it will be obvious that the method can be applied to any n-gon.
With the Z-wheel compass arc lengths can be measured and angles can be trisected. The trisection depends upon making a circle which has a radius 3 times the length of our original circle. The z-wheel is then rotated around the first circle from point A to point B and the arc distance noted from the wheel.. Then that same distance is marked 3 times upon the circle whose circumference is 3 times a large as the original circle, and the angle is trisected. (See Mr. Watt's geometry pages for a thorough and much more precise explanation of the compass, as well as an overhauling of Euclidian geometry, at http://www.compasswatt.com).
The 9-gon (in light green) -- formed by multiplying the radius
of the
original circle by 3.
Central angle (AGH) 360 / 9 = 40
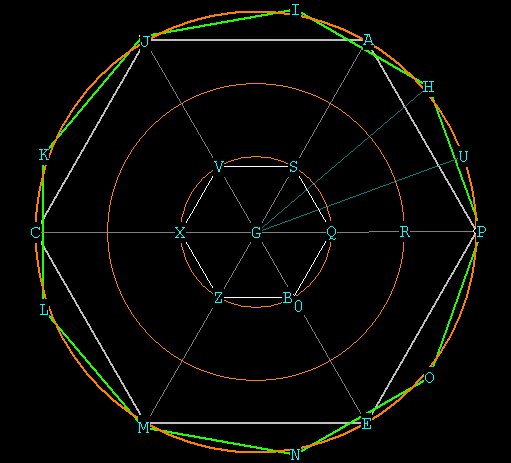
Our original circle is the inner circle with radius GQ. GQ is
considered to be Unity with respect to the other radial
distances. We
have divided into the circle with radius GQ to form the hexagon marked
in
white, which we shall use as a reference as we expand outward.
Place the
point of the compass at Q, to get R, and draw the circle with radius
GR. Pin
the compass at R to get P, and draw the circle with radius GP. Walk the
compass
around circle GP to get the hexagon marked in gray. We now have 3
circles such
that the radial distance of GR is exactly twice that of GQ, and the
radial
distance GP is precisely three times that of GQ.
The central angles of the hexagon (for example, <AGP) are all 60
degrees
(360 / 6 points of the heaxagon ). In order to get the 9-gon, we
have to
come up with a 40 degree angle. The best way to do that is to work with
the
hexagon, and cut the <AGP in thirds.
Take the z-wheel and pin it at G, with the other leg at Q. Then roll
the
z-wheel to S and note the distance on the wheel. With the compass still
pinned
at G, set the other leg now to P. Roll off the exact distance you
marked on the
inner circle (QS) from P on the outer circle until you hit U on the
outer
circle. Do the same from U to H and from H to A. Now you have cut
<AGP in
thirds and you have <PGU = <PGH = <PGA = 20 degrees.
So <PGH = 40 degrees, which is the central angle of the 9-gon (360 /
9 =
40). So the first two points on the 9- gon are P and H. Now you
can walk
either the standard compass or the Z-wheel compass around the circle to
get all
of the other points.
Now lets take on the 7-gon (heptagon). Here is a pic of it:
Normally we draw our circle and create the polygon inside of it.
Using the
z-wheel compass, we must use increasing radial distances. here is how
it is
done:
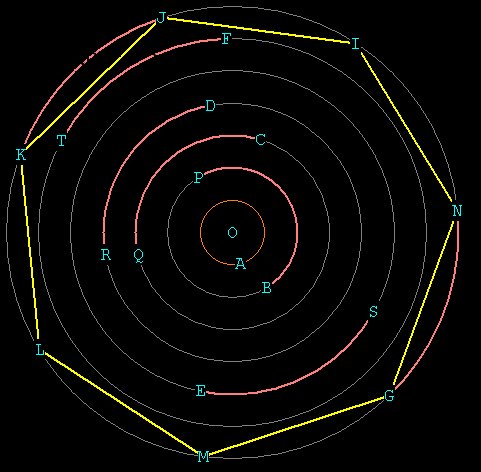
We will call the original circle A. We use it's radial distance OA
as Unity,
from which to derive all of the other distances. As before, we
use the
compass to get all of the other circles, which now have radii in
integer
multiples of the original circle OA.
We need to get 7 EXACTLY spaced points on the circumference of one of
the
circles in order to precisely generate the heptagon.
Firstly, note that the circumference of a circle is directly
proportional to the
radius of a circle:
C = 2PI*r. If the radius increases by whole number increments, then the
circumference also increases by that same amount: Lets compare
the circle
with radial distance OB, which has radius twice that of Unity, (so OB
=
2), to circle OF with radius 6:
C(F) = __2*PI*6__
= 3.
So C(F) = 3* C(B) if the radius is increased 3 times.
C(B) = 2*PI*2
Take the z-wheel compass and pin it at O. Start at A and make 1
complete
revolution of the compass wheel until you get back to A again. Note the
position on the wheel. We now have, logically, an exact distance for
the
circumference of circle A. Now all we need to do is go out to circle G,
with
the compass still pinned at O, and rotate the z-wheel 7 times with the
exact
arc-distance noted on the wheel to find our 7 points.
I have noted in orange how the exact circumference of circle A is
marked off on
all of the other circles: the circumferential distance of circle
A is
exactly one half that of circle B, exactly one third that of
circle C,
etc.
This ingenious solution does not require the use of PI or even messy
central
angles, it is dependent upon whole number radial distances. The wheel
itself
contains PI built right into it!
You can see that ANY n-gon can be constructed using this method: at
worst it
will take n concentric circles to draw any n-gon.
In the 9-gon we only needed 3 circles, because the 60 degree angle on
circle A
marks out a circumferential distance only 1/3 the distance on
circle C.
Now we come to one of the most talked about problems in 2 dimensional geometry, squaring the circle. Again, this is impossible with the standard compass but not with the Z-wheel compass. By simply tracing the arc length along the wheel and noting how many revolutions, one can simply detach the measuring leg and trace out the linear distance from the Z-wheel in a straight line. Two bisections of this distance give the length of each side of the square.
______________________________________________________________
Appendix and credits:
(1) paraphrased from Dr. Wilkinson at the Math Forum:
The great mathematician Carl Gauss discovered that a polygon with n
sides can
only be constructed if n is a power of 2, and if n is a prime
number of
the form 2^2^k + 1, where k is a positive integer.
for k = 0,1,2,3,4 we get 3,5,17,257,65537. For 2^k where k =
2,3,4 we get
4,8,16.
Looking just at the numbers from 3 to 20, the following table can be
shown
of which regular polygons can and can't be constructed:
3
yes
3 = 2^2^0 + 1
4
yes
4 = 2^2
5
yes
5 = 2^2^1 + 1
6
yes
6 = 2 * 3
7 no
8
yes
8 = 2^3
9 no
10
yes 10 =
2 * 5
11 no
12
yes 12 =
2^2 * 3
13 no
14 no
15
yes 15 =
3 * 5
16
yes 16 =
2^4
17
yes 17 =
2^2^2 + 1
18 no
19 no
20
yes 20 =
2^2 * 5
(2) From the paper called "Repairing a Deficiency in Euclidian
Geometry" by James Watt available at www.compasswatt.com:
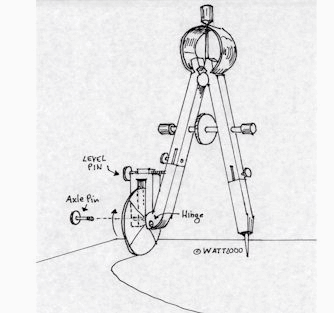
"At [top] is a drawing of such an
attachment which I call the "Z Compass. The Z wheel is placed on
the
curve at some intersection on the curve (or straight line) and is then
rolled
to the next point for marking. The rolling is the curvilinear
equivalent to
opening a rectilinear compass's legs. One can now transfer some
curvilinear
distance to another point in the construction. This is not using a
pre-existing
"marked ruler", nor is it a "mechanical devise", any more
than a compass is. If it is permissible to use a 2
dimensional
compass, why would it not be permissible to use a 3 dimensional
compass,
particularly given Euclidean geometry extensively examines both aspects
of
geometry? It is contrary to logic not to do so. The simplest version of
this
tool is a wheel pinned to a stick. The wheel is serving as a "3
dimensional
compass". It is a tool based on my postulate substitution for Euclid's
postulate 5 (see my geometry definitions at geometry
definitions).
The marks arrived at are from a "Rusty compass" (picking up the
compass and moving it) format, which is allowed in Euclidean Geometry
(i.e.
Euclid's "Classic Solution" to drawing parallel lines).
"An example of its use; We draw a circle and find its hexagonal points. An unmarked "Z wheel" is placed in the leg and the compass legs are registered to the radius distance. A beginning mark is made on the wheel and the wheel is rolled along the circumference until it meets the first intersection of hexagonal leg and circumference. Another mark is made to notate the distance traveled along the curve by some portion of the Z wheel. That portion notated, is the exact curvilinear distance of the hexagonal arc transferred from the original circle to the Z wheel. The Z wheel can be moved to another section of the construction or the legs swung open to another radial proportion and the measure of the relative hexagonal arc of one circle transferred to a completely different arc. For the first time, one is directly measuring relative arcs in geometric construction and doing so without numbers, which is of primary concern in Euclidean geometry.
"It is a case of what is good for
the
goose is sauce for the gander. One cannot claim objectivity, allow
rectilinear
distance recording and then disallow curvilinear distance recording. To
do so
makes your study in logic irrelevant... "