The underlying assumptions  in metaphysical geometry are as follows:
(See " The Creation of a Universe ").
0) Pure Awareness creates and perceives through  its creations.
1) Awareness is different from consciousness. Awareness is pure potential, a quality, not a quantity, with the ability to create matter and energy.
2) Consciousness is awareness perceiving through a vehicle of perception. The level or scope of consciousness is dependent upon the sensors built- in to the perception vehicle. For example, a human perceives differently than an amoeba, because their sensory equipment is different.
3) Consciousness is dependent upon perception of existence. Awareness is not dependent upon existence, awareness is the creator of existence.
4) Awareness is not IN existence, it is the creator of existence. Therefore, awareness encompasses the whole of existence, everywhere and all at once.
5) All discrete entities in existence, from cells to humans to galaxies, are conscious perceivers.
6) The fundamental 'particle' or quanta of energy in the universe is a thought. I will call this a POINT to distinguish it from 'thought,' which word has connotations I do not want associated with this discussion.
7) All matter and energy is ultimately composed of POINTS, which are created 'particles' of consciousness. All matter and energy exists within a universal 'soup' of awareness.
8) A POINT is the fundamental 'particle' of creation of awareness. The POINT can be used by awareness as the most basic  portal or platform from which to perceive.
9) POINTs can perceive  omni-directionally.
POINTS  have consciousness, atoms have consciousness, quarks have consciousness, rocks, trees, insects and humans have consciousness. This means that beer cans have consciousness. EVERYTHING in the universe is conscious, because everything in the universe is the product of Pure Awareness.
10) Energy, matter and all forms in existence are constructed by agreements between the conscious aggregates that comprise them. So, for example, a tetrahedron has 4 vertices and all four of them consciously agree to come together in the tetrahedral form.
11) The universe is held together by agreements between units of consciousness.
12) The universe is  dynamic because consciousnes is dynamic.
13) Everything in the universe is responsive to consciousness.
 

A POINT is defined as a place from which to perceive.
A POINT  is awareness perceiving through a position in space. It is dynamic, not static.
A POINT is  the building block of the universe of matter and energy. Let us say that it is the smallest possible unit of existence.
A POINT has consciousness and the ability to perceive around it.
A POINT is not an abstraction, it has consciousness and existence.

A LINE is formed when a perceiver becomes aware of another point. A LINE is  the connection of awareness between 2 POINTS. It comes about from a perceiver either creating a POINT, or becoming aware of something  other-than-itself already in existence.  It is NOT an infinite number of non-existent things!
A LINE is either curved or straight. If it is straight then there is instant communication. By that I mean there is no time between a communication from one end and the receipt of that communication at the other. A straight line can be defined by two POINTS, and there is no change of direction.
If the line is curved then there is a point within the concave boundary of the line from which all the other points are generated and to which they are all related. The arc of a circle is an example of a curved line. The center of the circle is the point to which all of the other points on the circumference are related, even though these points are constantly changing direction. Curved lines are always continuously changing direction.
A straight line represents communication. It represents relationship. It represents agreement.
A curved line represents something which can be perceived.

Communication (straight line) is instantaneous, perception is not, because  change of direction (curved line) requires a decision at every step along the way, a slight hesitancy which creates time. The awareness which composes all of the POINTS which comprise an object has many many possible directions  in which it can go. These explorations of consciousness within the object itself creates the persistence of the object.

Physics and chemistry shows there are no continuous surfaces in nature. All surfaces which appear continuous to the human eye are composed of bonded energy loci. The collections of energy (vertices) in any structure are held together by the consciousness of each locus of energy. These invisible bonds represent straight lines in the structure and they are pathways of communication and agreement between vertices.
Without the lines of communication betwen the vertices, the structure could not exist. It is the agreement between locally clumped-together-energy (vertices) which gives the structure its form and holds it together.
Each vertex is conscious and is aware of the other vertices.
In geometry, any polyhedron is composed of vertices, edges, and faces. The vertices represent the conscious energy loci, the edges represent the straight-line communication (agreement) between the vertices to precisely position themselves, and the faces represent the potential for dynamic change in the structure.

                                               2 Dimensional Geometry
The ancients used only compass and straight-edge for their geometric drawings. The idea is that the truth is simple, elegant and powerful, and so if we are thinking clearly and are connected to the source of universal truth, we should be able to demonstrate the universe with simple tools.

A note on central angles: a central angle is the angle a point makes with the center of the circle and an adjacent point on the circumference. If you look at the diagrams below, you will see that the central angle is also a measure of the chord length of the polygon (the side of the polygon).

Assertions:
All polygons are inscribed in circles. The circle is the beginning point for ALL 2  dimensional geometry.
The circle is  Unity.
Growth comes from the division of Unity.
The circle provides the reference point from which geometric order proceeds. In other words, all Form  is created from Unity.
Multiplication proceeds from division.
 

Let's say you are Pure Awareness. There is nothing in the universe, becaue nothing has been created yet. Lets say that as a creator, you decide that the boundaries of your universe will be at a distance r from you. As soon as you decide that, you have thunk a thought, a thought that is about a somethingness-which-is-other-than-you, which in turn creates a space between you and it. You have just created a POINT! Lets call that POINT A.
A

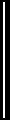
O
OA = r
 So now you have a radius, a limiting point of perception.  All of the points you will create, up to and including length r, will be your universe. You can have a 'soup' of consciousness, filled with POINTs, each of which is conscious, the outer boundary of which represents the  circumference of the circle of your awareness (we are only talking 2 dimensions here). For our purposes we will deal only with points on the circumference.

A circle -- your universe.

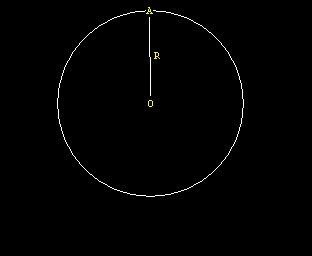
The only information you have is r. You are  O.  What can you do with that?
Pick a spot, any spot, on the circumference. Let that be A. Perceive through  A and create another POINT the same distance r from A. Call that B. Look in the other direction rom A and create another POINT the same distance, r, at C. Do the same while perceiving at C to create D, and at D to create E.
Magically, the 6 points, A,B,C,D,E,F are all exactly spaced around the circumference! This is your first realization about how cool creation can be.
If you are doing this with compass straight-edge and paper, start by pinning the compass at A, with length OA, and find the intersection with the  circumference at B  and C. Pin the compass  at B and find another point of intersection with the circumference at D . Pin the compass at C and find another point of intersection at E. From E (or  D)  find F.

The hexagon -- the first regular polygon in your universe. Central angle (AOC) 360 / 6 = 60

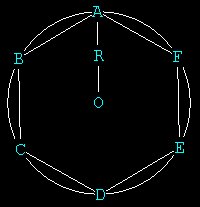
We have divided the circle into 6 parts and have created 6 points and 6 lines.
The lines in our diagram represent the communication between each conscious POINT in our hexagon. Each POINT agrees to be in precise relationship with the other POINTs. The distance R represents the limit of the awareness of the creator of the hexagon, us, at O. We are Pure Awareness. We have created the POINTs   A,B,C,D,E through our thought. We are at the center of it all -- we are in control of it all. Becaue the POINTS A,B,C,D,E  have been created by us, they have a little bit of our conscious awareness 'built in' to them, as an inherent part of their nature. They can be used by us as positions from which to view the hexagon from any POINT.
When we place our awareness at any POINT we see the exact same thing, because all of the distances are equal around the circumference and to the center..

We are now at F.   From F with the straight-edge connect to B and C. We have now created our second regular polygon, the equilateral triangle.
The triangle is the minimum polygon, with 3 vertices.
From A connect to D and E. Now we have, inscribed in the circle, 2 interlocking equilateral triangles. When we look at this figure 3 dimensionally later, it will be 2 interlocking -tetrahedron's forming the vertices of a cube.

The circumscribed Equilateral Triangle -- the minimum  polygon in your universe
Central angle (AOE)   360 / 3 = 120

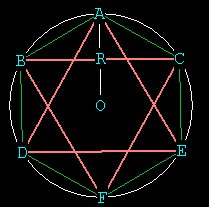
The first regular polygon in creation, then is the hexagon! This seems counter intuitive, doesn't it? How could something with 6 vertices come before something with 3 vertices? Of course you can stop after the first 3 points A, B, C and connect them to form a triangle, but this triangle is uninteresting because it doesn't have equal sides. Remember, all we know so far distance-wise is r, the radius! Connecting B and C requires us to think a new thought and we only know  r right now.
We could  have connected immediately to O after making B and formed an equilateral triangle. But this would involve us as one of the vertices. The whole point in creating something is to have it be outside of you, so you can play with it! We  are really into 'walking' our compass around the circle and we dont want to start something else before we have completed our first creation.
So in the beginning, there is a circle, and then 6 points on the circle forming the hexagon. From the 6, immediately comes the 3.
As we gaze out upon our hexagon and our triangles we realize that the lines of communication to all 6 points form 6 smaller equilateral triangles all with side lengths equal to r. We realize that the triangle is the simplest polygon and that 6 equilateral triangles could form a hexagon.
The hexagon is created from only one piece of data -- the decision to create something a distance R from ourselves.
 

We are on a roll now. We have now created a  regular polygon with 6 vertices and one with 3. Lets try and see if we can construct one with 4 vertices.  After  a little thought we figure it out. First with your straight-edge connect up points A and F. That's the easy part. We now have the 'y axis.' To get the 'x axis' we have to figure out how to bisect the lines BD and CE.
We still have our compass set to r! Pin it at B and draw and arc above BD. Pin it at D and draw and arc to intersect the first one. Now do the same  with the line  CE. Now with the straight-edge connect the two points together, going through O.
The intersection of this line with the circle comes at H and at I. The line IH is called a perpendicular bisector of the line AF, through O. Now IH is our 'x axis.'

Bisecting the line   xx'---

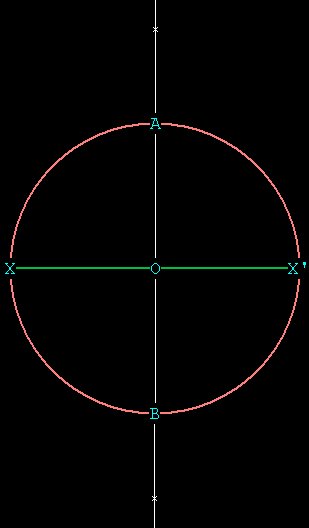
Pin the compass at x with the other leg at x', and mark an arc above and below the circle.
Pin the compass at x' with the other leg at x, and mark an arc above and below the circle that intersects with the other arc.  Now connect the line through O.
 

Now connect A, I, F, H to form the square. We can see that these points are regularly spaced because the angles between them are equal.

The Square  --- representing the earth Central angle(AOH) = 360 / 4  = 90

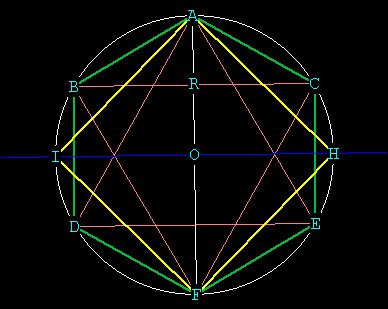
We have created 2 more points I and H and now have 4 polygons, a heaxagon (green), 2 equilateral triangles, (pink), and a square (yellow). Here we see that growth comes from further division into Unity.
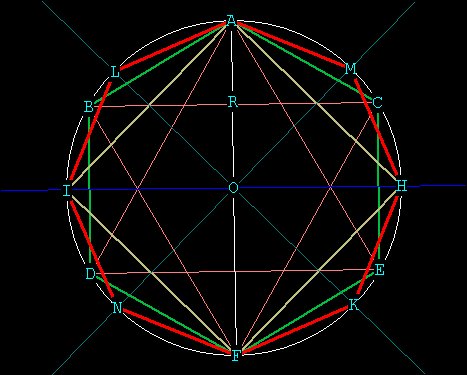
Now that we have our square, we can proceed to the 8 sided polygon, or octagon.
All we have to do is bisect each one of the sides of the square, which is the same thing as bisecting the central angles of the square.  We bisect lines AI and FH through O, and bisect lines AH and IF through O, to get points L,M,N, K

The octagon -- formed from the square (the octagon is in red). Central angle (MOH) 360/8 = 45

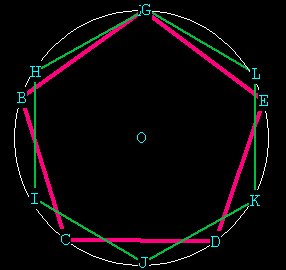
Now lets try for the 5-sided polygon to complete sequence of 3,4,5,6.
This one is a little tricky and requires a lot of thought. When we draw this one we have one explosive realization after another. See " The Construction of the Pentagon " for instructions and lots of information.

The Pentagon ---  representing continuous harmonic growth. Central angle (GOE) = 360/5 = 72

From the pentagon we can immediately get the 10-gon, or decagon, by bisecting the sides (and angles) of the pentagon, just like we bisected the sides of the square to get the octagon. It turns out that the sides of the decagon are in Phi ratio to the sides of the pentagon!

The decagon --   formed from the pentagon. Central angle VOU = 360 / 10 = 36

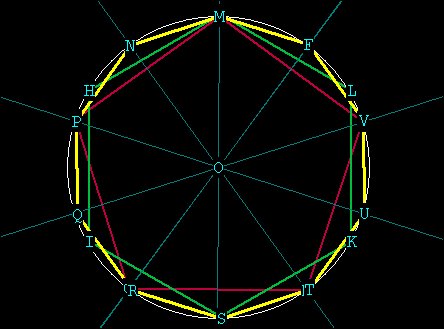
Here we have demonstrated all of the polygons from 3 to 10 that can be precisely generated in one and only one circle. There are 2 polygons  which are currently thought to be accurately impossible to draw geometrically:  the 7-gon (heptagon) and the 9-gon (enneagon). The 7-gon is impossible to construct because the central angles which represent its edges are repeating decimals
(i.e. 360 / 7 = 51.428571428571..... this number can't be pinned down).
The 9-gon can't be constructed, even though its central angle is an integer (360 / 9 = 40) because it involves the trisection of a 60 degree angle. Think about it.  We need a 40 central angle. We don't have protractors with nice little angles marked off on them, only compass and straight-edge.
So we have to work with an already-defined central angle. We have the following angles from the diagrams shown above:
120, 90, 72, 60, 45, 36.
The problem:   How to get 40 from any of these?
The only possible way is to trisect either the 120 (120 / 3 = 40) or
trisect the 60 (60 / 3 = 20. 20 + 20 = 40). But with the standard compass and straight-edge, we can only bisect!!  If you don't believe it is possible to trisect and angle, get out your paper, compass and straight-edge and try it for yourself!
It turns out we can only construct polygons of 2,4,5,6,8,10,12,15,16, 17,20 sides if we use standard compass and straight-edge. (1)

However, the 7-gon and the 9-gon, in fact ANY polygon can be constructed using the ingenious new compass developed by James D. Watt called the Z-wheel.
The Z-wheel  is attached to the marking leg of a standard compass and is used to measure arc lengths. This is such a simple concept, its amazing no one ever thought of it before. But that's what genius is, I guess.
In footnote (2) below  is a picture of Mr. Watt's compass, taken from his website, with a brief description.
With this compass ANY n-gon can be constructed by the simple, powerful and elegant method of multiplication of radial distances. In this method, PI is unnecessary. The unit of measure is simply the linear, whole number, radial distance which automatically generates a circumference. As we will show below, this is a brilliant idea and represents true genius. The only difficulty with this method is that it requires, in particular cases, n concentric circles to produce an n-sided polygon. But that doesn't detract from its power.
First lets start with the 9-gon, go to the 7-gon and then show and by that time it will be obvious that the method can be applied to any n-gon.

With the Z-wheel compass arc lengths can easily be measured and angles can  be tri-sected. The trisection depends upon making a circle which has a radius 3 times the length of our original circle. The z-wheel is then rotated around the first circle from point A to point B and the arc distance noted from the wheel.. Then that same distance is marked 3 times upon the circle whose circumference is 3 times a large as the original circle, and the angle is trisected. For those who object that the distance on the wheel is eyeballed, the same can be said of  the placement of ANY compass, anywhere, when doing geometry!  Geometry isn't about mechanical devices, it's about logic, and the logic of the 3 -dimensional compass is irrefutable. See Mr. Watt's geometry pages for a thorough and much more precise explanation of the compass, as well as an overhauling of Euclidian geometry, at http://www.compasswatt.com .

The 9-gon (in light green) -- formed by multiplying  the radius of the original circle by 3.
Central angle (AGH) 360 / 9 = 40

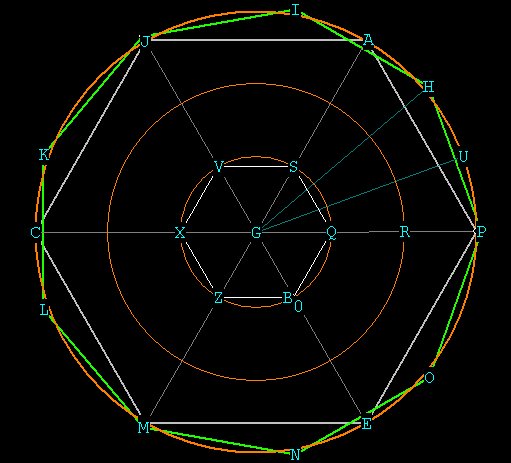
Our original circle is the inner circle with radius GQ.  GQ is considered to be Unity with respect to the other radial distances.  We have divided into the circle with radius GQ to form the hexagon marked in white, which we shall use as a reference as we expand outward.  Place the point of the compass at Q, to get R, and draw the circle with radius GR. Pin the compass at R to get P, and draw the circle with radius GP. Walk the compass around circle GP to get the hexagon marked in gray. We now have 3 circles such that the radial distance of GR is exactly twice that of GQ, and the radial distance GP is precisely three times that of GQ.
The central angles of the hexagon (for example, <AGP) are all 60 degrees (360 / 6 points of the heaxagon ).  In order to get the 9-gon, we have to come up with a 40 degree angle. The best way to do that is to work with the hexagon, and cut the <AGP in thirds.
Take the z-wheel and pin it at G, with the other leg at Q. Then roll the z-wheel to S and note the distance on the wheel. With the compass still pinned at G, set the other leg now to P. Roll off the exact distance you marked on the inner circle (QS) from P on the outer circle until you hit U on the outer circle. Do the same from U to H and from H to A. Now you have cut <AGP in thirds and you have <PGU = <PGH = <PGA = 20 degrees.
So <PGH = 40 degrees, which is the central angle of the 9-gon (360 / 9 = 40). So the first two points on the 9- gon  are P and H. Now you can walk either the standard compass or the Z-wheel compass around the circle to get all of the other points.
 

Now lets take on the 7-gon (heptagon). Here is a pic of it:

Normally we draw our circle and create the polygon inside of it. Using the z-wheel compass, we must use increasing radial distances. here is how it is done:

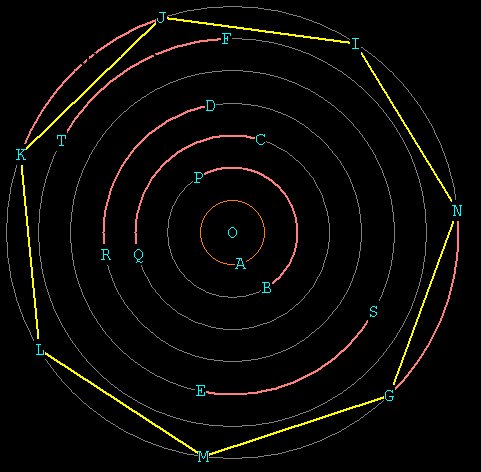
We will call the original circle A. We use it's radial distance OA as Unity, from which to derive all of the other distances.  As before, we use the compass to get all of the other circles, which now have radii in integer multiples of the original circle  OA.
We need to get 7 EXACTLY spaced points on the circumference of one of the circles in order to precisely generate the heptagon.
Firstly, note that the circumference of a circle is directly proportional to the radius of a circle:
C = 2PIr. If the radius increases by whole number increments, then the circumference also increases by that same amount: Lets compare  the circle with radial distance OB, which has radius twice that of Unity, (so OB =  2),  to  circle OF with radius 6:
C(F)  =      __2*PI*6__ =  3. So C(F) = 3* C(B) if the radius is increased 3 times.
C(B) =          2*PI*2

Take the z-wheel compass and pin it at O. Start at A and make 1 complete revolution of the compass wheel until you get back to A again. Note the position on the wheel. We now have, logically, an EXACT distance for the circumference of circle A. Now all we need to do is go out to circle G, with the compass still pinned at O, and rotate the z-wheel 7 times with the exact arc-distance noted on the wheel to find our 7 points.
I have noted in orange how the exact circumference of circle A is marked off on all of the other circles:  the circumferential distance of circle A is exactly one half that of circle B,  exactly one third that of circle C, etc.
This ingenious solution does not require the use of PI or even messy central angles, it is dependent upon whole number radial distances. The wheel itself contains PI built right into it!
Of course this solution will be objected to on the grounds that it is impossible to manufacture a perfectly circular wheel, but the same can be said about  any object anywhere in existence. The placement of any regular compass involves eyeballing and hand placement anyway, so all geometry is inherently, mechanically messy. Geometry is more about logic and the discovery of truth about the physical universe. The z-wheel compass helps us in our discoveries.

You can see that ANY n-gon can be constructed using this method: at worst it will take n concentric circles to draw any n-gon.
In the 9-gon we only needed 3 circles, because the 60 degree angle on circle A marks out a circumferential distance  only 1/3 the distance on circle C.
 

Now we come to one of the most talked about problems in 2 dimensional geometry, squaring the circle. Again, this is impossible with the standard compass but not with the Z-wheel compass. By simply tracing the arc length along the wheel and noting how many revolutions, one can simply detach the measuring leg and trace out the linear distance from the Z-wheel in a straight line.  Two bisections of this distance give the length of each side of the square.
______________________________________________________________
Appendix and credits:

(1) paraphrased from Dr. Wilkinson at the Math Forum:
The great mathematician Carl Gauss discovered that a polygon with n sides can only be constructed if n is a power of 2, and if n is a  prime number of the form 2^2^k + 1, where k is a positive integer.
for k = 0,1,2,3,4  we get 3,5,17,257,65537. For 2^k where k = 2,3,4 we get 4,8,16.
Looking just at the numbers from 3 to 20, the following table can be shown
of which regular polygons can and can't be constructed:
       3    yes    3 = 2^2^0 + 1
       4    yes    4 = 2^2
       5    yes    5 = 2^2^1 + 1
       6    yes    6 = 2 * 3
       7    no
       8    yes    8 = 2^3
       9    no
      10    yes    10 = 2 * 5
      11    no
      12    yes    12 = 2^2 * 3
      13    no
      14    no
      15    yes    15 = 3 * 5
      16    yes    16 = 2^4
      17    yes    17 = 2^2^2 + 1
      18    no
      19    no
      20    yes    20 = 2^2 * 5

(2) From the paper called "Repairing a Deficiency in Euclidian Geometry" by James Watt available at www.compasswatt.com:
 "The Greeks disallowed "mechanical means" in their method of geometry. It has already been demonstrated that the curve is superior to the straight line. It is not possible to know anything about a straight line (1 dimension) except that it is acted upon by a compass and curved line (2 dimensions). It is therefore reasonable to postulate the study of 2-dimensional form is best accomplished from a 3-dimensional aspect, in keeping with solution by hierarchy of dimensional technique. Nor should this go against pre-existing Greek criteria. They themselves, routinely worked in 2 and 3 dimensions and it is true, but unarticulated, that a 2 dimensional line must be used to study a 1 dimensional line. What is missing, artificially and detrimentally in Euclidean geometry, is a "Z compass for an XY curve." A compass which records and transfers arcs- as well as radii.

 

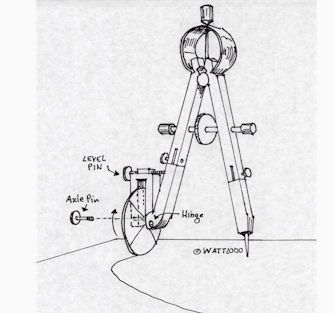
"At left is a drawing of such an attachment which I call the "Z Compass.  The Z wheel is placed on the curve at some intersection on the curve (or straight line) and is then rolled to the next point for marking. The rolling is the curvilinear equivalent to opening a rectilinear compass's legs. One can now transfer some curvilinear distance to another point in the construction. This is not using a pre-existing "marked ruler", nor is it a "mechanical devise", any more than a compass is.   If it is permissible to use a 2 dimensional compass, why would it not be permissible to use a 3 dimensional compass, particularly given Euclidean geometry extensively examines both aspects of geometry? It is contrary to logic not to do so. The simplest version of this tool is a wheel pinned to a stick. The wheel is serving as a "3 dimensional compass". It is a tool based on my postulate substitution for Euclid's postulate 5 (see my geometry definitions at geometry definitions). The marks arrived at are from a "Rusty compass" (picking up the compass and moving it) format, which is allowed in Euclidean Geometry (i.e. Euclid's "Classic Solution" to drawing parallel lines).

"An example of its use; We draw a circle and find its hexagonal points. An unmarked "Z wheel" is placed in the leg and the compass legs are registered to the radius distance. A beginning mark is made on the wheel and the wheel is rolled along the circumference until it meets the first intersection of hexagonal leg and circumference. Another mark is made to notate the distance traveled along the curve by some portion of the Z wheel. That portion notated, is the exact curvilinear distance of the hexagonal arc transferred from the original circle to the Z wheel. The Z wheel can be moved to another section of the construction or the legs swung open to another radial proportion and the measure of the relative hexagonal arc of one circle transferred to a completely different arc. For the first time, one is directly measuring relative arcs in geometric construction and doing so without numbers, which is of primary concern in Euclidean geometry.

"It is a case of what is good for the goose is sauce for the gander. One cannot claim objectivity, allow rectilinear distance recording and then disallow curvilinear distance recording. To do so makes your study in logic irrelevant. This is a 26 centuries old problem here clearly identified for the first time and it should be fixed. The benefit of such a consideration are immediate and stunning. "