Having Fun With Geometry
3 Dimensional Geometry
We will proceed in 3 dimensions as
we did in two dimensions.
Let’s reintroduce Hal from the previous article, a being who is self
aware
before the universe was created (hey, I told you I was having fun with
this!)
Hal has already created a bunch of 2 dimensional polygons, and now he
is ready
for something new.
Hal decides to start all over again and so he makes another POINT at A
and
moves it about himself, 360 degrees, to create another circle:
Figure 1
After a bit of thought, Hal gets the
bright idea to 'flip' the circle over himself. When he does this he is
astonished
to have created a uniformly symmetrical cocoon of energy that
completely
surrounds himself, and he decides to call it a sphere.

Figure 2
This excellent animation (1) was taken from the U.S. Naval
Observatory (2).
Even though it is an animation of the phases of the moon, it serves to
show how
a circle rotated about it's center 180 degrees will form a sphere.
Here’s
another look at it:

What can Hal do next? Well, the
limit of his universe is now a sphere in 3 spatial dimensions. He can
start
filling in his sphere with a bunch of POINTs, but he’s pretty excited
about his
new creation and wants to see what the sphere looks like from the
outside. So
Hal decides to look straight up and he locates POINT A; and from there
he
creates another sphere with center at A (because that’s all he knows
how to do
right now), shown in red. I’ve drawn the spheres as circles because I
don’t
want to clutter the diagrams, but think of them as spheres.
When he does this the 2 spheres
intersect each other. like so:
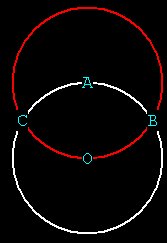
Figure 3
We have now created 2 intersecting points on the outside of the
original
sphere, at the outer edges of the sphere with center at A. Lets call
these
POINTs B and C. If this were a 3D pic you could see more clearly
the
intersections of the 2 spheres. It forms a football shape called a
vesica.
Hal recognizes that he could create another hexagon from the
intersections of
six spheres, so he goes to B and in turn C, creating two more spheres,
and
finding POINTs D and E.
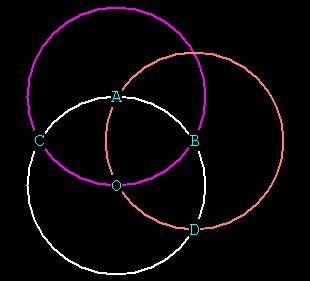
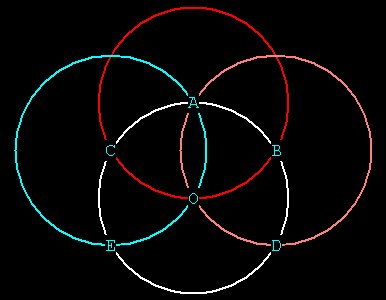
Figure 4
If Hal continues around the original circle and draws spheres at D and
E, he
finds one more point F.
Then drawing a circle at F we complete the circuit:
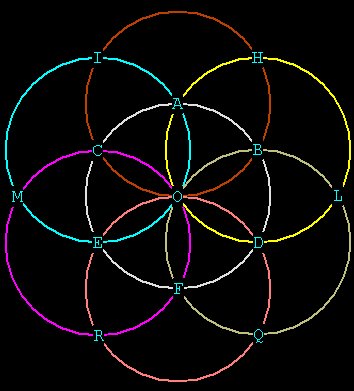
Figure 5
Hal thinks this looks pretty cool, so he goes out to one of the 6 spheres he created on top of the original sphere at A, and does the same thing. In fact, he can continue this process indefinitely. Soon he’s got a nice looking pattern:
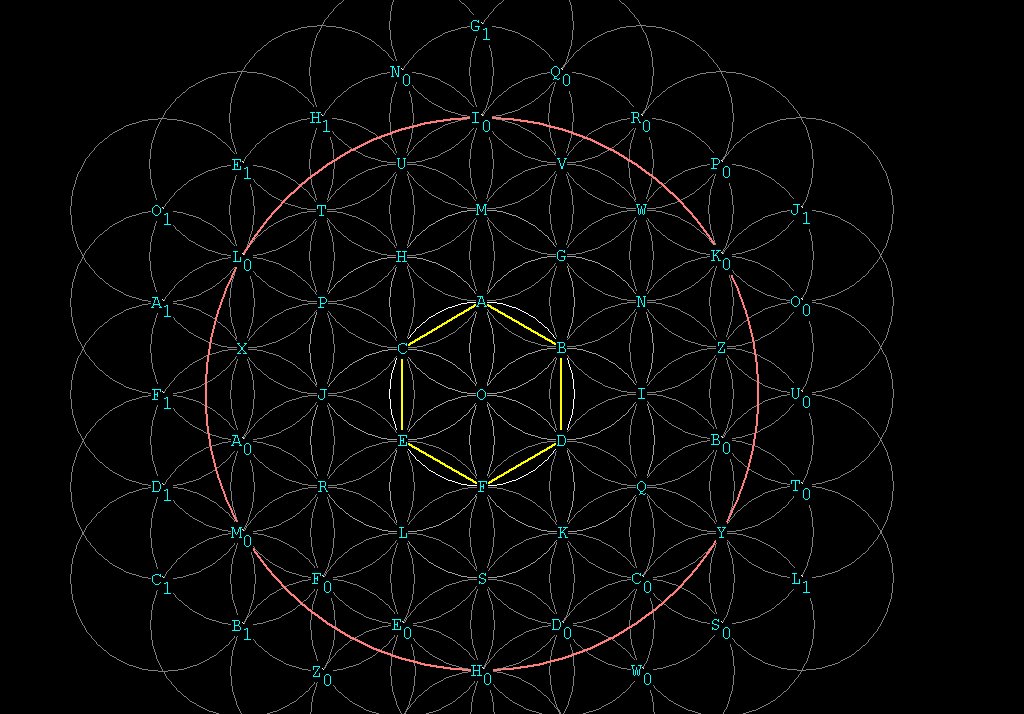
Figure 6 -- The intersecting sphere
pattern. This is a poor representation, being only 2 dimensional. You
have to
imagine spheres piled on top, and below the plane of the paper or
monitor
screen.
Notice that there are 2 sizes of
vesicas in the pattern above: the smaller (e.g. from O to F)
and the larger (e.g. from O to C to A to B). The ratio between the long
axis
(CB)
and the short axis (OA) is \/¯3. The ratio between the
long and
short axis of the smaller vesica's is 2 + \/¯3.
(See Maths Page ).
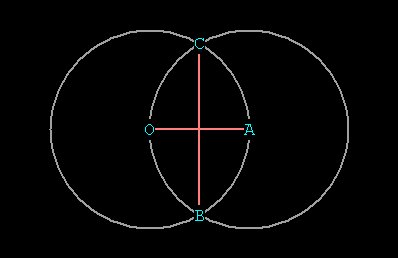
Figure 7 -- a vesica, the intersection of 2 spheres

A vesica, marked in blue.
Why is this pattern so significant?
Well for one thing, if you remove every sphere with a center on the
surface
another sphere, so that the spheres do not intersect, but only touch on
their
surfaces, you have a pattern of tangent, or 'closest packed' spheres:
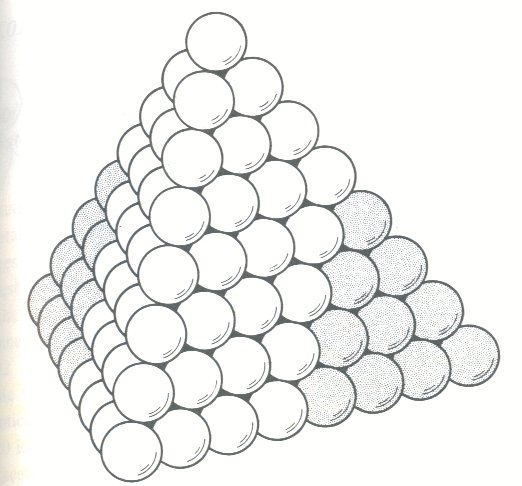
If you stack cannonballs, or ping pong balls, or any spheres so that
they
nestle together with the most packing efficiency (90.69%), you get a
cubic closest
packed lattice.
This pattern of tangent spheres is Buckminster Fuller's Isotropic
Vector
Matrix, shown below in another form, with the spheres removed and the
connecting LINEs from their centers:

(3)
Figure 7B – The
Isotropic Vector
Matrix. It is made by connecting the sphere centers in a closest packed
lattice.
From this pattern, Hal can see 3
of the 5
Regular Solids,
the tetrahedron, the octahedron, the cube, and also the cubeoctahedron.
In 3 dimensions, there are 12 spheres surrounding each sphere. If you
look at
Figure 7B, there are twelve struts which come out from each vertex.
The pattern of intersecting spheres
that Hal made, and the Isotropic Vector Matrix, is constructed so that
the
angles between the central sphere at O, and any of the 12 spheres that
branch
out from it, are 60 degrees.
Basically, it consists of interlocking octahedrons and tetrahedrons,
which
completely fill space:
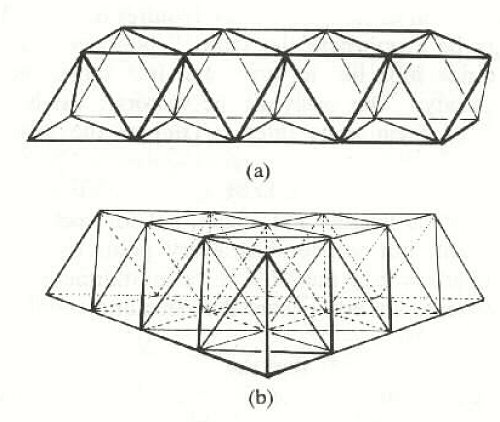
Figure 7C (4)
Figure 7D below shows the
12-spheres-around-1. Fuller called it a Vector Equilibrium and it is
also
called a cubeoctahedron. The top of the cubeoctahedron is shown in
bright
yellow, the bottom half in lighter yellow, and the central sphere is at
O. A
cubeoctahedron is formed by cutting off the corners of a cube.
You may be able to visualize this if you imagine 6 spheres coming
outward
toward you, with centers at H3, I3, and L3, and 3 spheres below,
at F3,
K3, and J3, (sitting 'above' the pattern. There are also 6 spheres
whose
centers form a hexagon surrounding the central sphere. I’ve marked
these 6
spheres in orange:

Figure 7D -- the cubeoctahedron in 3D
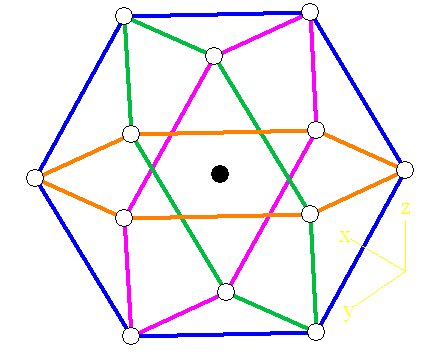
Another look at the cubeoctahedron.
Hal has found 4 polyhedra (poly =
many, hedra = faces) already, but he has noticed that all of them have
faces
which are either triangular (3 sided) or square (4 sided):


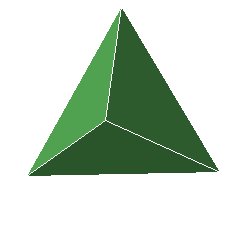
Figure 8 (cube, octahedron,
tetrahedron)
He wonders whether there are any
solids which have pentagonal (5 sided) faces?
First he discovers the icosahedron:
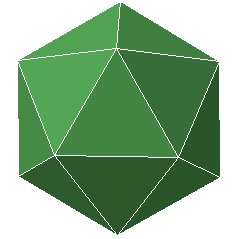
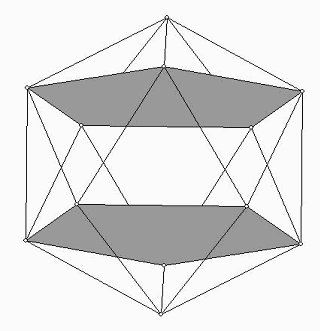
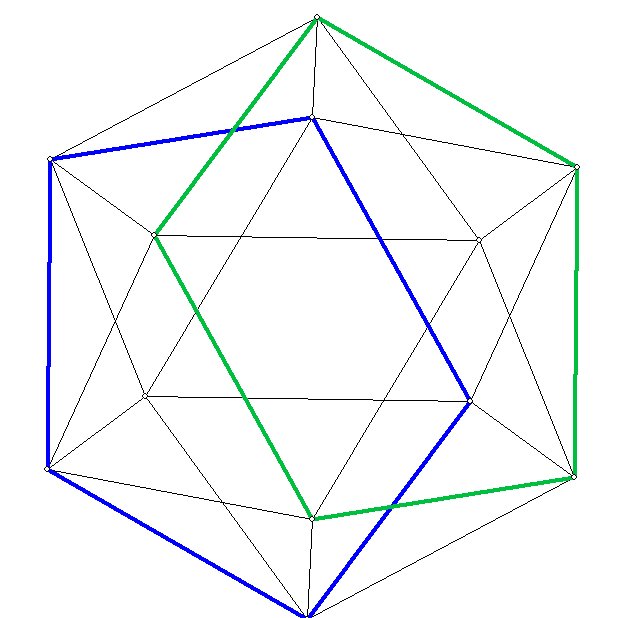
Figure 9
and notices that although it has triangular faces, it is composed of
pentagons
inside, and pentagonal caps on the outside, as shown above.
He notices that if he takes out the central sphere in the 12-around-1
(cubeoctahedron), he gets the icosahedron:
Figure 10
Here the cubeoctahedron (left) “jitterbugs” into the icosahedron
(right).
No matter how hard he tries, Hal,
although a very brilliant being, can’t discover a 3 dimensional solid
with
pentagonal faces that fits into the pattern, until he does this:
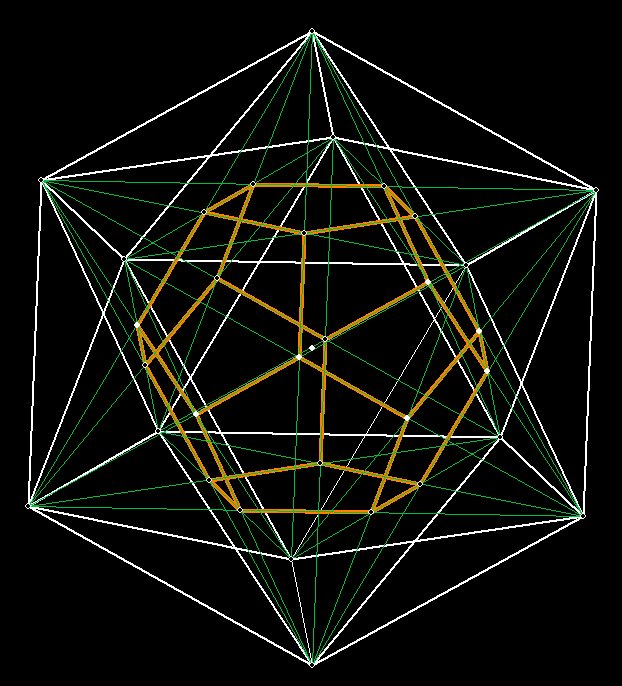
Figure 11
Hal draws a LINE from every one of the vertices of the icosahedron to a
non-adjacent vertex, except for those that go through the middle, and
marks the
intersection POINTs. When he connects up the LINEs to adjacent POINTs,
viola!
He winds up with the dodecahedron, a solid which has faces that are
pentagons.
The vertices of the dodecahedron can also be found by orienting 5 Tetrahedrons, like so:
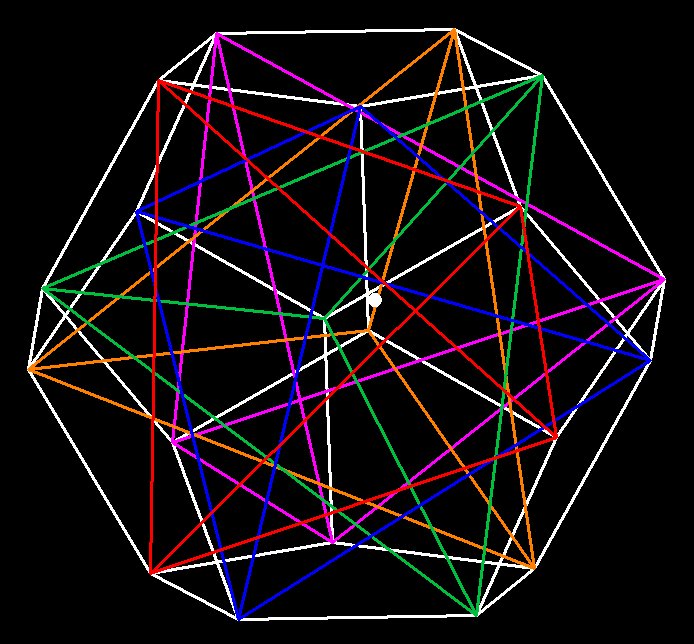
Figure
12 –
Dodecahedron from 5 tetrahedrons. There are 20 vertices to a
dodecahedron, and
4 for every tetrahedron. 4 x 5 = 20.
Hal discovers something else about
the pattern he’s made. It’s 2 dimensional representation, a bunch of
intersecting circles, can be flipped over to form 3 dimensional torii:
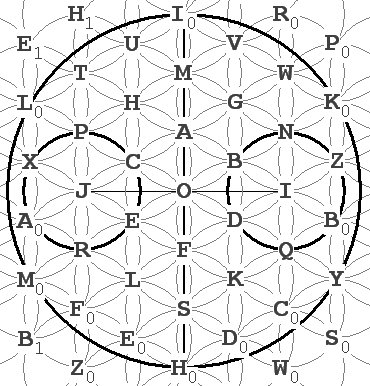
Figure 12 If Hal rotates either of the two circles at J and I around
the axis
IH, a ring torus will form:
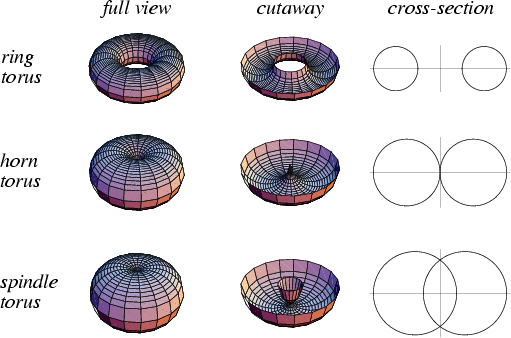 (5)
(5)
Figure 13 – The three standard
torii, showing cross-sections. Note that since Hal’s pattern is
symmetrical,
torii of any size may be created. A 3 dimensional vesica can be seen in
the
spindle torus.
We could go on, but we’re not! We’re
going to leave Hal, as he is busy creating more and more geometric
figures and
doesn’t have time for us anymore. Now, all we have to do is wait 13
billion
years, and hopefully he’ll be smart enough to have created the rest of
the
universe.
_____________________________________________________________________
Geometry is an important subject
because it involves the spatial relationships between every object in
the universe, andt it’s also important to biology. Look at the
nucleotide, shown below:
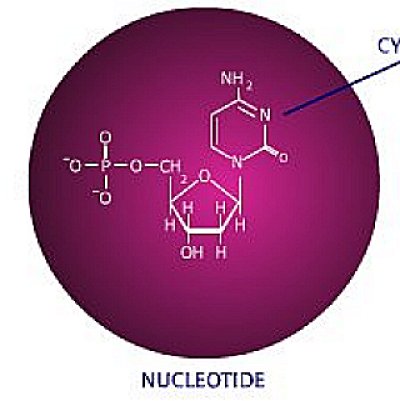 (6)
(6)
Figure 15 The nucleotide –
the building block of DNA.
The phosphate group (to the left) is square,
the deoxyribose-sugar is pentagonal, and the nitrogenous
base to the right is hexagonally shaped.
The Dodecahedron is even more difficult to contruct because it is composed entirely of pentagons. For that reason, this structure must be intimately associated with biological life.
The main idea is that we can make
any possible geometric shape, either directly, or indirectly, from the
intersecting sphere pattern. (I have just shown the 5 regular solids
here).
Even though the dodecahedron and the icosahedron must always remain
slightly
imperfect (or any shape which has Ø within its makeup), by
altering the
radius of the spheres and superimposing interlocking sphere
patterns one
over the other, all of the forms we observe in existence can be
constructed.
_________________________________________________________________
References:
(0) Geometric drawings done
using R. Parris's free 'peanut' software at
http://math.exeter.edu/rparris/default.html
(1) GIF animation by Ed Stephan (stephan@cc.wwu.edu) from
U.S.
Naval Observatory page at:
(2) http://tycho.usno.navy.mil/vphase.html
(3) This vrml version of Fuller’s
IVM from Richard Hawkins Digital Archive.
(4) This image is from Amy Edmundson’s Fuller Explanation at
www.angelfire.com.
(5) from http://mathworld.wolfram.com/Torus.html, "Eric Weisstein's
World
of Mathematics."
(6) from http://www.dnaftb.org/dnaftb/ Section 15 of 'DNA From
the
Beginning'.