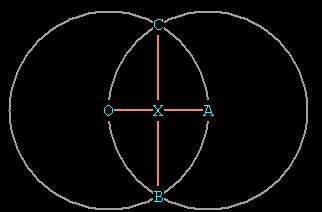
Figure 1 --- A large vesica
Large vesica properties:

Figure 1 --- A large vesica
Let the radius of each circle = 1. Then notice OB = OA = OC =
AC = AB = radius = 1.
Also notice CB bisects OA. So OX = CB = 1/2.
By Pythagorean Theorem, CX² = CA² - XA² = 1 -
¼ = 3/4.
So CX = \/¯3 / 2. CB = CX + XB so CX =
\/¯3/2 + \/¯3/2 = \/¯3.
Small vesica properties:
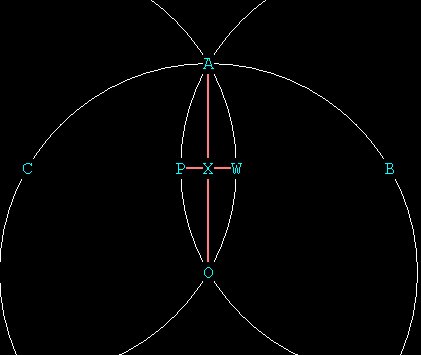
Figure 2 ---- two views of the small vesica OA. OA has been drawn with major and minor axes as with the large vesica above.
Notice that there is a sphere at C and one at B. We already know from
above that the long axis of the large vesica (OCAB) is \/¯3.
The distance from C to W (located at the right edge of the sphere
centered at C) is 1, because it is the radius. Similarly for the distance
BP, for the sphere centered at B. A line AO will bisect a line CB,
so that X is the midpoint between C and B.
So we have :
C_________(_X_)_________B
P W
distance CX = distance XB = \/¯3/2. This is the same distance
we found for CX of the large vesica in Figure 1.
Distance CW = 1 because it's the radius of C.
Therefore distance XW = 1 - \/¯3/2, or, (2 -
\/¯3) / 2.
Distance PW = twice distance XW, so the short axis of the
small vesica is 2 - \/¯3.
So the ratio of the long axis to the small axis in the smaller vesica
is: 1 / (2 - \/¯3)
= 2 + \/¯3.
(Note that (2 - \/¯3) * (2 + \/¯3) = 1. So multiplying
both numerator and denominator by
2 + \/¯3 gives 2 + \/¯3).
Special characters:
\/¯ ² ³ × ½ ¼ Ø
\/¯(ز + 1)