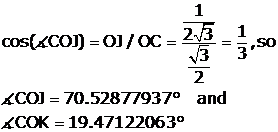The Star Tetrahedron
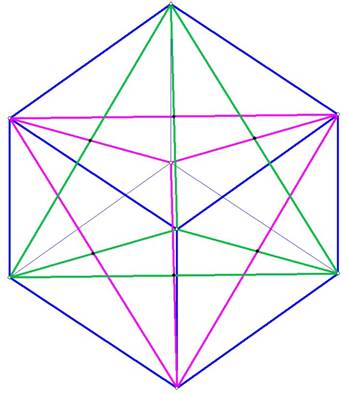
Figure 1. The Star Tetrahedron in the Cube
Figure 1 shows the cube in blue, and two interlocking tetrahedrons, one in purple, the other in green. To visualize this, imagine that the green tetrahedron comes out of the page at the top front corner of the cube and the purple tetrahedron goes back toward the bottom corner of the cube, into the page.
The two interlocking tetrahedrons each intersect the other by bisecting each othersí sides. This becomes much clearer when you build a 3D model.
 †
†
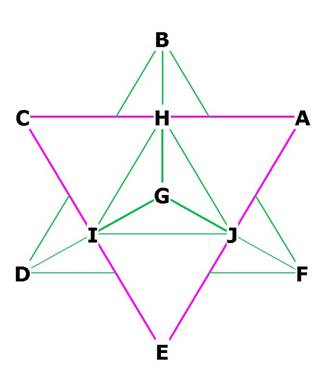
Figure 1A
Figure 1A shows that the interlocking tetrahedra bisect the sides of each other. BG bisect CA at H, FG bisects AE at J, DG
bisects CE at I. There are 12 interlocking edges, 6 for each tetrahedron.
What is the volume occupied by a star tetrahedron inside a cube?
The intersection of the two interlocking tetrahedrons forms an octahedron plus
8 smaller tetrahedronís that stick out from the octahedron, as shown below.
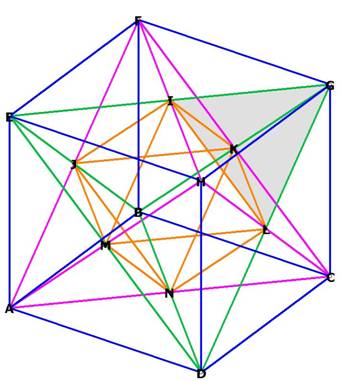
Figure 1B
Shopwing the 8 smaller tetrahedron that stick out
from the octahedron, one from each of the octahedral faces. I have shaded one
of these tertahedra (GILK).
The volume of the star tetrahedron is the volume of the octahedron + volume of
each small tetrahedron, so we write:
![]()
Let s = side of the cube = 1. Then ![]()
The length of the edges of the interlocking tetrahedrons are each
![]() * side of the cube, because each of them is a diagonal of a
square face of the cube.
* side of the cube, because each of them is a diagonal of a
square face of the cube.
The edges of each of the small tetrahedrons are exactly 1/2 side of the large
tetrahedron, because each of the large tetrahedrons bisects the other in order
to form the interior octahedron. That is the magic of the Platonic Solids!
So the sides of the small tetrahedron = ![]() †
†
The sides of the interior octahedron are also ![]() , because the vertices of the octahedron bisect the edges of
the interlocking tetrahedrons. This becomes clear when you build a three
dimensional model.
, because the vertices of the octahedron bisect the edges of
the interlocking tetrahedrons. This becomes clear when you build a three
dimensional model.
We know from Octahedron that the volume of an Octahedron is ![]() †We need to convert
this to the side of the cube:
†We need to convert
this to the side of the cube:
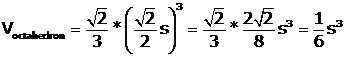 , where s = side of cube.
, where s = side of cube.
We know from Tetrahedron that the volume of a Tetrahedron is ![]() . It turns out that the edge lengths of each of our 8
tetrahedrons is equal to the lengths of the sides of the octahedron. So we may
write
. It turns out that the edge lengths of each of our 8
tetrahedrons is equal to the lengths of the sides of the octahedron. So we may
write
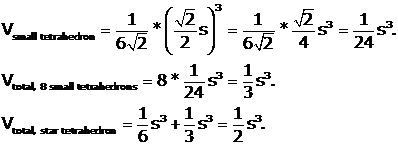 †
†
Even though the volume of each large tetrahedron in the star tetrahedron is
exactly 1 / 3 of the cube, the star tetrahedron only occupies one half the
volume of the cube.
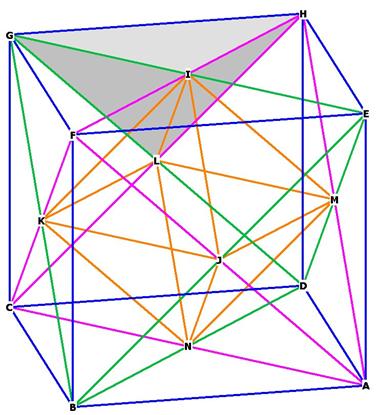
Figure 2. There are 8 congruent solids (for example, GLHI) representing the
left over space in the cube not included in the star tetrahedron volume.
Since the left over space in the cube = ![]() ,
,
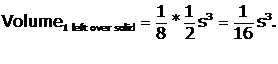 .
.
These solids have 4 vertices, 4 faces, and 6 edges, thus fulfilling the Euler
requirement that
Faces + Vertices = Edges + 2.
The Star Tetrahedron in the Sphere
The sphere enclosing the star tetrahedron is the same sphere that encloses the cube.
The diameter of the enclosing sphere is the distance marked in orange in Figure 4, with the centroid of the star tetrahedron marked with a black dot:
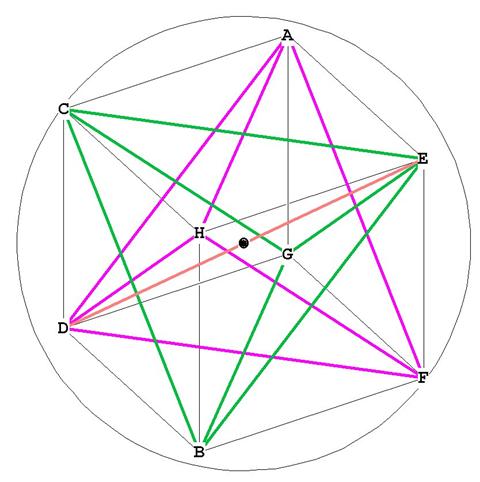
Figure 3†
All 8 points of the star tetrahedron touch the surface of the enclosing sphere.
Note that the diameter of the enclosing sphere is the same diagonal that goes
through the center of the cube. In Figure 3 this is marked as ED. From Cube we know
that the length of this diagonal, and the diameter of the enclosing sphere, is ![]() . (This calculation is a simple one, ED being the hypotenuse
of the right triangle EDF. Since DF is the diagonal of the cube with sides = 1,
DF =
. (This calculation is a simple one, ED being the hypotenuse
of the right triangle EDF. Since DF is the diagonal of the cube with sides = 1,
DF = ![]() . FE = 1, because itís the side of the cube, so by the
Pythagorean Theorem, ED =
. FE = 1, because itís the side of the cube, so by the
Pythagorean Theorem, ED =![]() ).
).
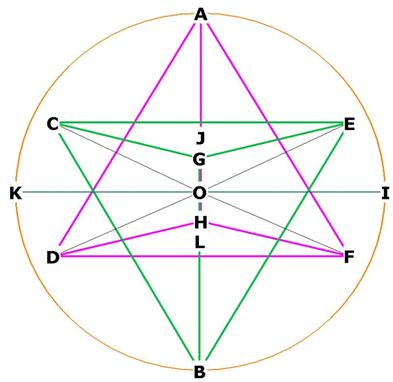
Figure 4. A different view of the star tetrahedron
There are 4 axes of rotation for the star tetrahedron; AB, CF, DE, and GH.
Notice the planes CGE in green and HDF in purple; both planes go into and out
of the screen or page.
What is the distance between these planes?† This distance will† be the line
JOL. J lies at the center of CGE, and L lies at the center of HDF. O is the centroid. By construction, both planes are parallel to each
other.
What is the angle between the xy plane at the
origin and the planes CGE and HDF? This will be ![]() IOE, for example.
IOE, for example.
It turns out that if you have a model of the star tetrahedron you can easily
see that the distance between the two planes, JOL, is the height of one of the
smaller tetrahedrons from the previous section.
We know that the height of a tetrahedron is ![]() †* side of tetrahedron
=
†* side of tetrahedron
= ![]() .
.
JOL = ![]() s. This distance is exactly 1/3 of the diameter of the
enclosing sphere.
s. This distance is exactly 1/3 of the diameter of the
enclosing sphere.
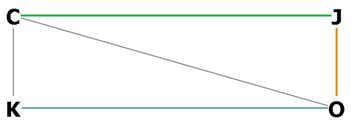
Figure 5. Showing JO, the distance between the plane CGE and the centroid O.
JO = one half of JOL =![]() s.
s.
CJ represents the plane CGE and OK represents the plane DFH. J is the center of
the plane CGE, and L is the center of the plane DFH.
CO is the radius of the enclosing sphere, and equal to![]() s.
s.
Now we have OJ and CO and can get the angle COJ: