The Decagon
The decagon is an amazing polygon. There are many
fascinating relationships within it.
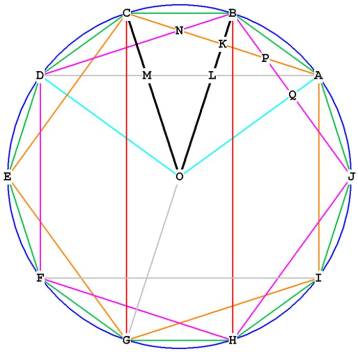
Notice that the decagon is composed of two interlocking pentagons, BDFHJ in
purple, and
ACEGI, in orange.
We already know the relationship between the radius of the pentagon and the
pentagon side, so what is the relationship between the side of the decagon and
the radius?
Between the side of the decagon and the side of the pentagon?
We know that OA = OB = OC = OD = radius of circle
around decagon/pentagon.
We know, from Pentagon Construction that OD = OB = radius, is the
distance from center to a vertex of the pentagon, and that is
Inverting this, we know also that side of pentagon = .
We also know from this paper that OK = * side of pentagon.
To find AB, the side of the decagon, let's work with triangle BKA.
We know AK to be 1/2 * AC, because OB is a bisector of AC.
Then
And AB = side of decagon =
Side of pentagon =
So side of decagon = =
Therefore the triangle COB, and all of the others like it, are Golden Mean Triangles.
What is DA in terms of the decagon side
(ds)? (Pentagon side = ps).
To get this ,we work with triangle DAI.
We know DI, the diameter of the circle surrounding the decagon, or twice the
radius.
We also know AI, the side of the pentagon.
So we can write:
What is CG = BH? (This is the diagonal of
any of the inscribed pentagons).
We will be working with triangle BGH.
We know BG, the diameter or twice the radius, and we know GH = side of decagon.
There are some interesting relationships in the
decagon.
Let's start by showing that triangle AOM similar to triangle DOL.
1) DAF = ADI because they subtend equal arcs DF and
AI.
2) OD = OA because they are both radii of the circle with center at
O.
3) OM = OL because ML is parallel to CB and triangle OML similar to
triangle OCB by A-A-A.
Therefore the triangles AOM and DOL are similar by angle-side-side.
Therefore AM = DL.
Since AM = DL and both lines are divided by the equal
distance ML, DM = AL.
Now we show that triangles ALO and DMO are
congruent.
1) AL = DM
2) DO = AO as they are both radii of the circle centered at O.
3) OM = OL as above.
Therefore the triangles ALO and DMO are congruent by side-side-side.
So AL = OL = DM = OM.
We can write:
LM is to AL as AL is to AM.
Therefore the line AM is divided in Mean and Extreme Ratio at L.
And so the line DL is divided in Mean and Extreme Ratio at M.
ML also divides the line DA in Mean and Extreme
Ratio at M and L, so we can also write
AL is to AM as AM is to AD.
These are the same relationships and triangles we saw in the pentagon.
Although we have a lot of information, we still
haven't proven the following:
Is AM = AO? We have shown that triangles ALO and DMO are congruent, but not
that triangle AMO is isoscles.
But this is easily proven, because we know that LM is to MO as CB is to CO,
which we have seen, is the division into Mean and Extreme Ratio..
But MO = AL.
Therefore OM is to OC as AL is to AM, and so AM = OC.
So triangle AOM is isosceles.
Since OM is to AM as CB is to OC, then CB = OM.
Therefore triangle AOM congruent to triangle COB.
Also we know that CM = BL = LM.
We know that triangle BAL is a golden mean
triangle, since BA = AL, and
BL is to AB as CM is to CB, which is to say, a division in mean and extreme
ratio.
CAD = 1/2 that of BAD, because it subtends an arc exactly 1/2
as long.
Therefore AC is an angle bisector of BAD, and BK = BL.
*******************************************************
Let's show all these relationships with brute force calculation!
We will be working first with triangles OKA
and AKL.
OB is an angle bisector of <COA, so OB bisects AC at K, and BK = KL.
So OB is perpendicular to AC.
We have previously found BK in relationship to the side of the pentagon. Let's
convert this value to the side of the decagon:
We also found previously that
To find AL, write
AL = side of the decagon BC, as we stated above.
What is OL? If we are correct above, it should be
equal to AL and BC.
OL = OB - BL.
BL = BK + KL = 2 * BK =
OL = -
=
Therefore OL = the side of the decagon = AL = BC.
The relationship of OL to OB is therefore
We can show DM = AL with the same triangles
on the upper left of the decagon.
Since we know DA, we can write:
LM = DA - 2*AL
So by calculation,
and AM is divided in Mean and Extreme Ratio at L.
What is the relationship between AM and AD.
We said it was a relationship. Let's see.
AD / AM =
It isn't surprising that there are so many Phi relationships in the decagon, it being composed of 2 interlocking pentagons.
Let's summarize our knowledge with a table: (available in the book)
What about AP, BP, KP, and PQ?
Are there any Phi relationships there?
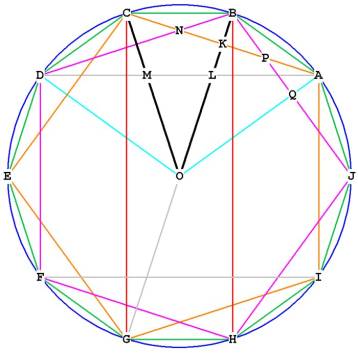
First let's show that triangle BKP is similar to triangle BQO.
1) OBQ is common to both triangles.
2) BKP and BQO are right.
3) Therefore, by the property that all angles of a triangle must add to 180°,
BPK = BOA.
So the triangles are similar by angle-angle-angle.
Now we can determine OQ in triangle BQO and from
there determine BP and KP.
BQ is 1/2 the side of the pentagon.
Now we can write:
BK is to BP as BQ is to OB, or, BK / BP = BQ / OB.
And
OQ is to OB as KP is to BP, or, OQ / OB = KP / BP,
BN = BP and KN = KP.
The relationship between BP and KP is .
It looks from the diagram that the sides of the pentagon, BD, BJ, and AC, when they hit each other at N and P, divide the side of the pentagon equally in fourths. But this is not so.
Lets add this information to our chart:
(available in the book).
