The Cube Octahedron
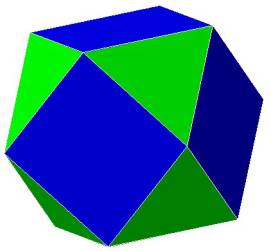
Figure 1
The cube octahedron is sometimes called the vector equilibrium. That is
what Buckminster Fuller called it.
It has 12 vertices, 14 faces, and 24 edges. It is made by cutting off the
corners of a cube.
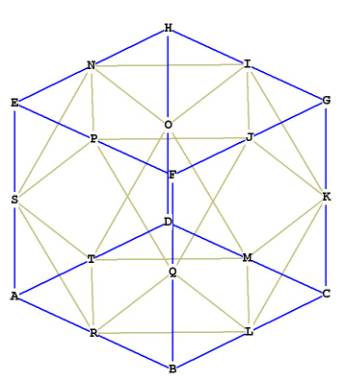
Figure 1A showing the cube octahedron (yellow) inside the cube (blue).
Notice that the triangular face of the cube octahedron IJK is formed by cutting
off the corner of the cube G, and that the square face of the cube octahedron
NPJI is formed when the 4 corners of the cube H,E,F, and G are cut off.
The cube octahedron has 8 triangular faces and 6 square faces. Figure 1 shows 3
of the square faces and 3 of the triangular faces.
There are 6 square faces on the cube octahedron, one for each face of the cube.
There are 8 triangular faces on the cube octahedron, one for each vertex of the
cube.
This polyhedron has the fascinating property that the radius of the enclosing
sphere, which touches all 12 vertices, is exactly equal to the length of all of
the sides of the cube octahedron. Unfortunately, our 2 dimensional perspective
cannot accurately capture the cube octahedron in true perspective, but if you
build a model of one you’ll see its true.
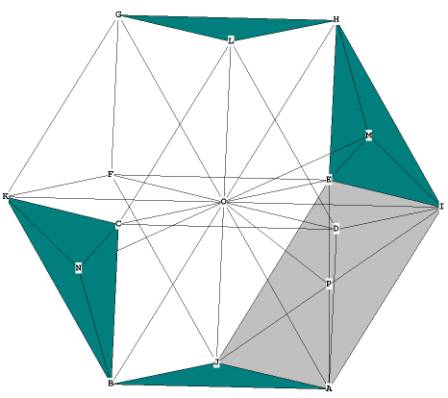
Figure 1B
In Figure 1B you can see some of the rays coming out from O, for example OB and
OA. These rays coming out from the center are all equal in length to the sides,
for example, GL and LC. This means that all of the rays branching out
from the centroid, O, do so at 60 degree angles, forming 4 'great circle'
hexagonal planes on the outside of the figure.
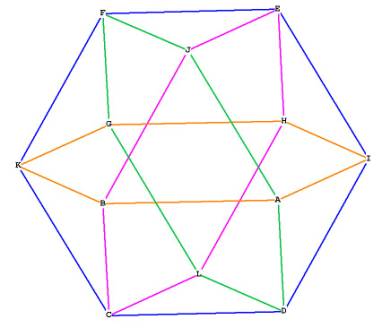
Figure 2 -- showing the 4 'great circle' hexagons
The cube octahedron, if you observe Figure 1C closely, can be seen to be
composed of 8 tetrahedrons and 6 half-octahedrons. OGLH and OJAB, for example,
are tetrahedrons. The half-octahedrons are formed from the square planes, for
example OEIAJ and OCKGL.
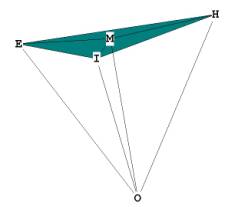
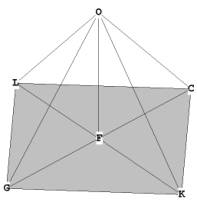
Figure 3 -- showing the tetrahedron and the half-octahedron,
which are also the 2 distinct pyramids of the cube octahedron.
The 12 vertices of the cube octahedron can also be considered to be composed
of 3 orthogonal squares centered around O, the sides of which cross
through the square faces of the cube octahedron as the diagonals of the
squares:
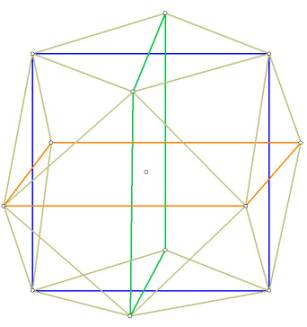
Figure 4 -- showing the 3 interlocking squares, the corners of which are the
vertices of the cube octahedron. Note how the sides of the squares are the
diagonals of the square faces of the cube octahedron.
Notice that in Figure 5 below, the intersection points of the squares form the
6 vertices of an octahedron:
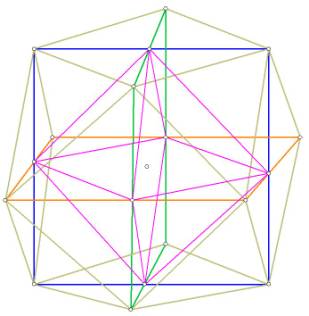
Figure 5. The diagonals of the cube octahedral “squares” intersect to form the
vertices of an octahedron (in purple)
What is the ratio of the radius of the enclosing sphere around the cube
octahedron, and the side of the cube octahedron?
r = s.
All line segments from the centroid to any vertex are identical in length to
the edge length’s.
What is the volume of the cube octahedron (hereinafter referred to as c.o.)?
We use the pyramid method as usual.
V = 1/3 * area of base * pyramid height.
We have 8 triangular faces and 6 square faces.
From The Equilateral Triangle we know that the
area of the triangular face is .
The area of the square face is just s * s = s².
We need to find the height of the square pyramid and the height of the
triangular pyramid.
In Figure 3, the triangular pyramid, or tetrahedron, is OEHI, with height
OM. Triangle OMH is right, the line OM being perpendicular to the plane EHI at
M. The height of the tetrahedral pyramid
is known, from Tetrahedron, as .
In Figure 3, F is the center of the square face LCKG, and OF is the pyramid
height. The triangle OFL is right, the line OF being perpendicular to the plane
LCKG at F. OL is just the radius of the enclosing sphere, which, in the
c.o., is the same as the c.o. side, s.
LF is one half the diagonal of the square LCKG, or ,
because the diagonal of a square is always times the side of the square.
Therefore we can write for the pyramid height OF, .
.
Note that this distance is identical to LF.
The Volume of 1 triangular pyramid then, is = .
The Volume of all 8 triangular pyramids is = .
The Volume of 1 square pyramid = = .
The Volume of all 6 square pyramids = 6 * = .
Therefore the Total Volume of the cube octahedron =
= 2.357022604 = 2.357022604 .
This figure is larger than for the cube, but why? The volume of the cube in the unit sphere is only 1.539600718 r³ ! The reason lies in the fact that the cube octahedron fits more snugly within the unit sphere than does the cube.
The model on my desk shows the cube octahedron inside the cube, as in Figure
1. Here, the side of the cube octahedron is This can be determined by an inspection of
triangle GIJ in Figure 1.
GI = GJ = 1/2 the side of the cube. Angle IGJ is right. Therefore, GJ, the side
of the cube octahedron = .
Calculating the volume of the cube octahedron in terms of the side of the cube
as in Figure 1, we write
Therefore the volume of the cubeoctahedron is 5/6ths the volume of the cube
when the edge length of the cubeoctahedron and the edge length of the cube are
the same.
There are 8 small tetrahedrons which represent the volume of the cube
octahedron that have been “cut out” of the cube (See Figure 1 and the tetrahedron
GKIJ, for example). The volume of each of these tetrahedrons must then be
one–eighth of 1/6, the difference between the volume of the cube and the volume
of the cube octahedron. Therefore the volume of each small tetrahedron = .
What is the surface area of the cube octahedron?
The surface area is 8 * area of triangular face + 6 * area of square face = .
What is the central angle of the cube octahedron? Each of the
internal angles of the c.o. are formed from any of the 4 hexagonal planes which
surround the centroid (see Figure 2).
Therefore the central angle of the cube octahedron = 60°.
There are 2 surface angles of the c.o., one being the 60° angle of the triangular faces, the other being the 90° angle of the square faces.
What is the dihedral angle of the cube octahedron? This angle is the
intersection between a square face and a triangular face. If you sit the c.o.
on one of its square faces you can see the following:
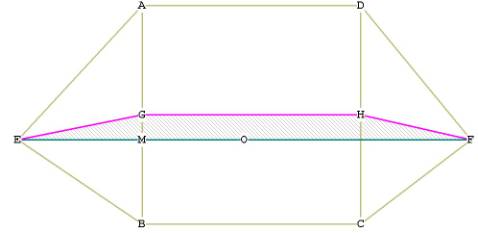
Figure 5 - illustrating the dihedral angle of the cube octahedron -- top
view
I have drawn the line EGHF to illustrate the dihedral angle between the two
triangular faces and the square face ABCD. The point G is directly above the
point M. O is the centroid of the c.o. M bisects EO.
The triangle GME is right by construction. The angle MGH is right by
construction. The angle EGH is the dihedral angle. If we can find the angle
EGM, all we have to do then is add 90° to it ( MGH), and we have the dihedral angle.
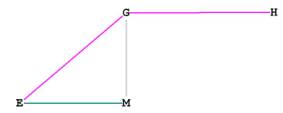
Figure 6 -- showing that GME and MGH are right angles
OE = OF = side of c.o., or s. EM = 1/2 * OE.
EG is the height of a triangular face, which we know from The Equilateral Triangle is .
So we can write:
sin( EGM) = EM / EG = .
= 35.26438968° .
EGH = 90° + 35.26438968° = 125.26438968°
.
Dihedral angle = 125.26438968° .
The distance from the centroid to each vertex = s = r.
The distance from the centroid to any mid-edge is just the height of an
equilateral triangle (remember that the centroid is surrounded by 4 hexagons
(Figure 2)). This distance is
The distance from the centroid to a triangular mid-face is just the height of
the tetrahedron (see Figure 3), which we know from above, as
The distance from the centroid to a square mid-face is just the height of the
half–octahedron OF (see Figure 3), which we know from above, is
The relationship between these distances is 1, 0.866025404, 0.816496581,
0.707106781
Cube Octahedron Reference Tables
(included in the book)
