We will use the intersecting circle/sphere pattern to construct  roots.
We will do this using simple right triangles.
The determination of the roots in this manner  is geometrically precise.
The determination of a root can be done almost by eyeballing the pattern.
Using this pattern, the easiest roots to construct, I have found, are the prime roots!
\/¯3 and \/¯7 figure prominently in the construction of roots, believe it or not.
The construction of higher and higher roots is made simpler by the use of roots lower in the table.
This paper will present the basic concept and show it with  diagrams .

Now please read " Introduction To The Pattern ."
 

Following is a table showing how to construct roots.
As we go higher and higher in the table, there are more and more ways to construct roots using the pattern. No doubt others will find more elegant ways to do so than are provided in the table.
1 = one radial distance in the pattern. For example, OB = 1.

root			alt	alt
(hypotenuse)	side 1	side 2	side 1	side 2
2	1	1
3	1 ½	\/¯3 / 2
4	2	0			1	\/¯3
5	2	1
6					2	\/¯2
7	2 ½  (2)	\/¯3 / 2  (\/¯3)
8	2	2	1	\/¯7
9	3	0	\/¯2	\/¯7
10	3	1
11			2	\/¯7	3	\/¯2
12					3	\/¯3
13	3 ½	\/¯3 / 2
14			\/¯7	\/¯7	2	\/¯10
15					2	\/¯11
16			3	\/¯7
17	4	1
18					3	3
19	4	\/¯3
20					\/¯10	\/¯10
21	4 ½	\/¯3 / 2
22					3	\/¯13
23			4	\/¯7
24
25	5	0
26
27	5	1
28
29	5	2
30
31	5 ½	\/¯3 / 2
32			5	\/¯7

The way to go about the determination of the root is as follows:
Pick any point in the pattern. I usually start from the center of a circle, but this is not required.
Get side 1 by going in any of the 6 directions indicated by the pattern and determining point 1.
Get side 2 by going at a right angle the necessary distance and finding point 2.
Connect your origin point to point 2 to find the hypotenuse. Draw a circle with radius equal to the hypotenuse. All points on this circle are the root distance from point of origin.

I will demonstrate the determination of the \/¯3, \/¯7, \/¯13.

\/¯3:
The Table shows \/¯3, side 1 = 1 1/2, side2 = \/¯3 / 2.
Start at O. Go 1 to F and then 1/2 more to find point K1. Now take a right angle and go
1/2 the distance along the large \/¯3 vesica LK, from K1 to K. Now simply connect OK and draw a circle with center at O.  I have marked this circle in yellow.
Notice that \/¯3  hits all of the vesica endpoints at L,J,H,G and I.

\/¯7:
The table shows \/¯7, side 1 = 2 1/2, side 2 = \/¯3 / 2.. Or,
                                 side 1 = 2      , side 2 = \/¯3.
Start at O. Go 2 to M and then 1/2 more to P1. Take a right angle \/¯3 / 2 and hit V.
Connect OV and draw circle.
Or, go 2 to M and \/¯3 to W, covering the entire \/¯3 vesica MW.
Connect OW to get the same circle.
Notice that \/¯7 fits elegantly into the pattern, hitting all vesica points at Z,W,V,U,T,X, etc.

\/¯13:
Start at O. Go 3 radial distances until you hit Lo, the 1/2 more to hit Q1.
Take a right angle from Q1 to hit E1. Connect OE1 and you have a circle with radius \/¯13.
Notice that again, \/¯13 elegantly hits vesica points at E1, A1, D1, etc.
 

The roots which fit most elegantly into the pattern are those which can be directly determined from the \/¯3.
Astonishingly ALL of the roots, prime or not, may be geometrically determined using the \/¯3.

This gets fun when you try more difficult roots.

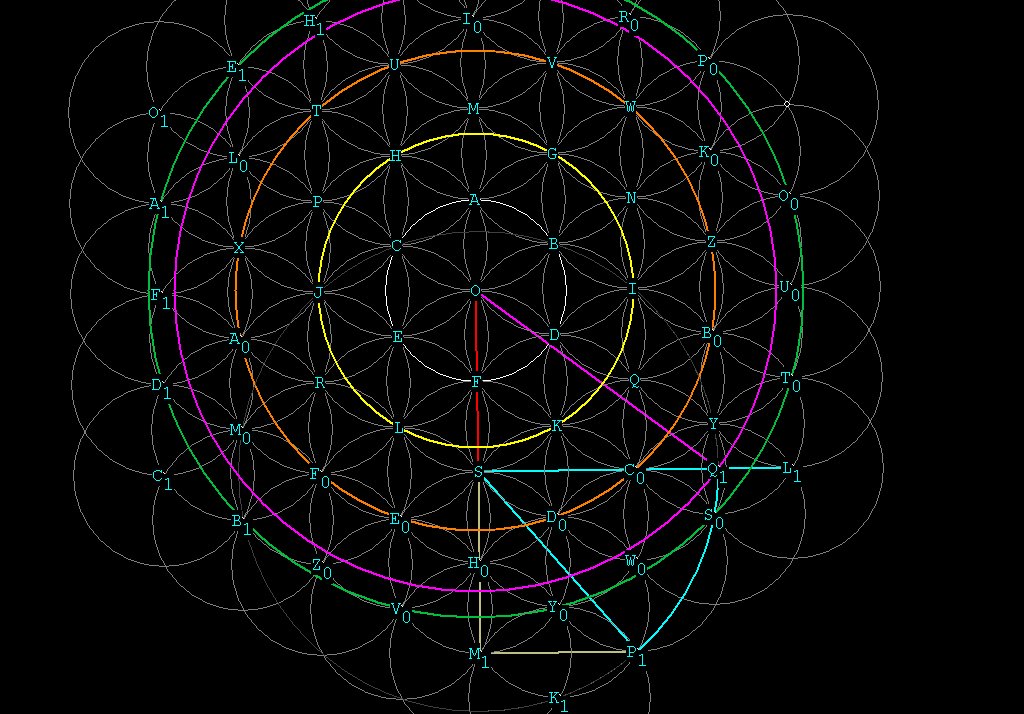
For instance, to get \/¯11, the table says to go 2 radial distances, to S, then at right angles a  distance equal to \/¯7. This sounds ludicrous until you try it!
\/¯7 elegantly fits into the pattern. Look up \/¯7 and you find it is just (2,\/¯3).
All you have to do is from S in which you went 2 radial distances, make a right triangle by going 2 more radial distances to M1 and then at right angles to that, go \/¯3 to P1. Connect up SP1 and you have \/¯7! I have highlighted SP1 in cyan. If you are using compass and straightedge,  pin your compass at S with length SP1 and draw an arc to intersect the line SL1, which is perpendicular to SM1 and thus at a right angle to SM1. You will hit Q1.
SQ1 = \/¯7, at a right angle to  OS and forming the long side of a right triangle OSQ1.
Now connect OQ1 and you have \/¯11!  A circle has been drawn in magenta to represent the \/¯11.

Determining and graphing square roots is amost trivial using this method.

The prime roots seem to be easier to graph and calculate than the others!
For example the \/¯19 requires one right triangle, but the \/¯20 requires two.
That is because the pattern is based on the \/¯3, which is friendlier to 19 than to 20.
Nevertheless, this method is a powerful (and fun!) way to graph any root.

Here are some interesting tidbits:

  The relationship between  Ø and the \/¯3:
   The Missing Link: The Ø to \/¯3 Conversion Triangle

  Some earlier thoughts on square roots
   The Square Root of 7

Special characters:
 \/¯ ­ ° ¹ ² ³ × ½ ¼ Ø  \/¯(ز + 1)