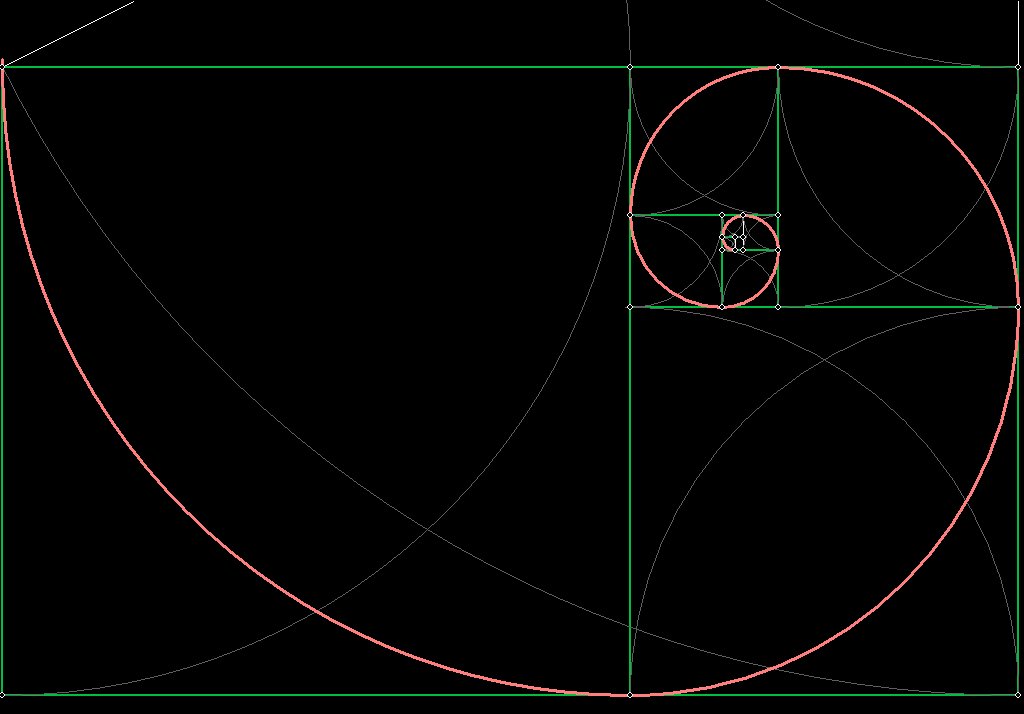
Figure 1 A Golden Mean Spiral
First we will show how to generate a Golden Mean Spiral geometrically. If you already know how to do this, keep going. If not, click here .
Below is the golden mean spiral, in orange:

Figure 1 A Golden Mean Spiral
Now lets try to find the equation of this spiral geometrically.
The origin will be at the bottom left, I have marked this out as (0,0)
in Figure 2 below. I have marked out some of the other relevant points
as well.
We want to find the distance from the center of the spiral to any point
on the curve.
But we have already said that the spiral never reaches the center!
That is true, but where the spiral cannot go, we can see that the intersection
of the 2 lines AI and HK, marked in grey, can mark the hypothetical center.
I have labeled that hypothetical center O.
So from O we can get a precise measurement of the distance to any point
on the curve.
We will call the distance from O to any point on the curve, r.
Clearly as the spiral rotates inward, r decreases, and when the
spiral rotates outward, r increases.
In order to find O we need to know the intersection of the 2 lines
AI and HK, relative to the point F, which is the origin of our coordinate
system.
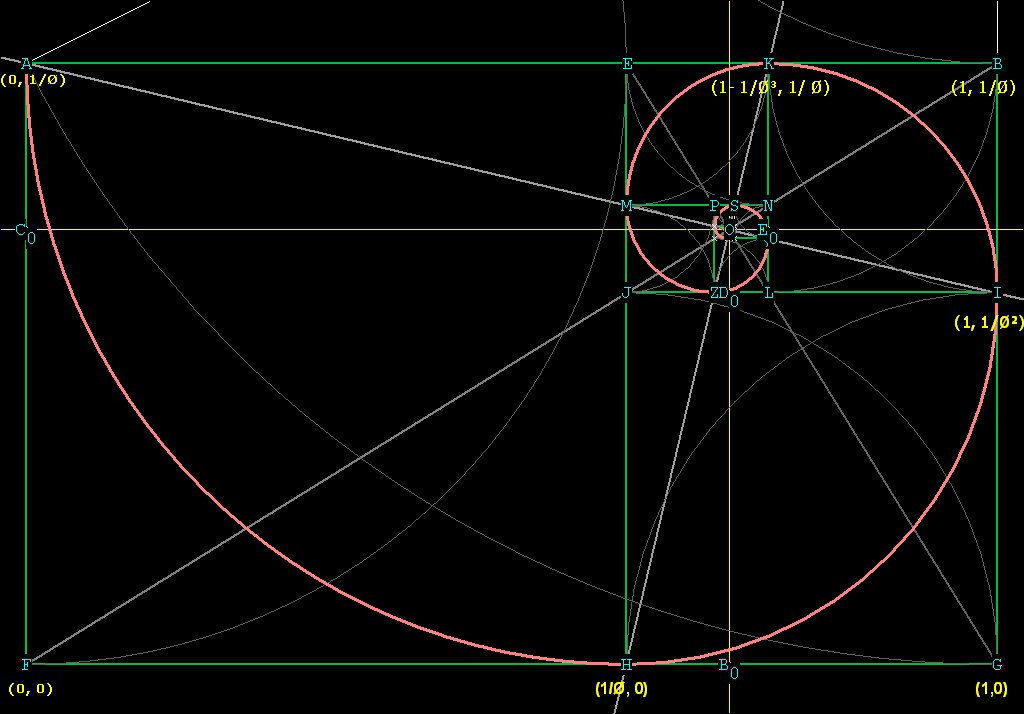
Figure 2
The slope of line AI is (1/ز - 1/Ø) / (1 - 0) = (1 - Ø) / ز = -1/س.
Comparing any 2 points on the line AI, we know they MUST be related
by the slope of the line.
Taking (x,y) as any point on the line AI, and using point A, we can
write for the equation of the line AI:
(y - 1/Ø) / (x - 0) = -1/س,
y = -1/سx + 1/Ø.
[1]
The slope of line HK is
(1/Ø - 0) / (1 - 1/س) - 1/Ø
= 1/Ø / {[(س - 1) / س] -1/Ø}
= 1/Ø / [(س - 1 - ز)
/ س] = 1/Ø / 1/Ø^4
= س.
So the equation of line HK (using point H) is
y / (x - 1/Ø) = س,
y = سx - ز.
[2]
The x coordinate of the intersection of the two lines is then
-1/سx + 1/Ø = سx - ز,
(س + 1/س)x = (س + 1) / Ø,
[(Ø^6 + 1) / س]x = (س + 1) / Ø,
x = (س + 1) / Ø * س /
(Ø^6
+ 1) = ز(س + 1) / (Ø^6 + 1)
= ز / (ز
+ 1).
Plugging x back into [2], we get
y = س(ز / (ز + 1)
- ز =
[Ø^5 / (ز + 1)] - ز =
(Ø^5 - Ø^4 - ز) / (ز + 1)
= Ø / (ز + 1).
The center of the spiral O is at [ز / (ز +
1), Ø / (ز + 1)],
relative to the origin (0,0) at point F.
(Notice that the relationship of the x distance to the y distance is Ø, so that the triangles FOBo and FOCo are phi triangles.)
Now that we have found the hypothetical center of the spiral, we can see how the distance from O to any point on the spiral changes.
Since we already have 4 points calculated, A, H, I, and K, lets find the distance of each of them from O, the center of the spiral:
To find OA, we need to know the coordinates of Co.
X is obviously 0, but Y is, from Figure 2, 1 / Ø
- the distance from the line FG to the center of the spiral, which we already
found to be Ø / (ز + 1).
So the y coordinate is 1 / Ø - Ø / (ز +
1) = 1 / Ø(ز + 1).
So Co is at (0, 1 / Ø(ز + 1)).
OA² = OCo² + CoA² = Ø^4 / (ز
+ 1)² + [1 / Ø(ز + 1)]² =
= Ø^4 / (ز + 1)² + 1 / ز(ز
+ 1)² =
= (Ø^6 + 1) / ز(ز + 1)²
=
= 2ز(ز + 1) / ز(ز +
1)² =
= 2 / (ز + 1)
OA = \/¯(2 / (ز + 1)).
To find OH we need to know the coordinate of Bo. This is easy, since
it has the x distance matching the center of the spiral.
So Bo is at (ز / (ز + 1), 0).
OH² = BoH² + OBo² = [(Ø
/ ز + 1)]² + [1 / ز(ز
+ 1)]²
= ز / (ز + 1)² + 1 / Ø^4(ز
+ 1)²
= (Ø^6 + 1) / Ø^4(ز + 1)²
= 2ز(ز + 1) / Ø^4(ز + 1)²
= 2 / ز(ز + 1)
OH = (1/Ø) \/¯(2 / (ز + 1)) .
To find OI we need to know the coordinates of Do. This is easy, since the x distance from the origin (0,0) is the same as Bo. The y distance is the same as for I, which is 1 / ز. So the coordinate of Do is (ز / (ز + 1), 1 / ز).
OI² = ODo² + DoI².
ODo = OBo - DoBo = Ø / (ز + 1) -
1 / ز = س - ز - 1 / ز(ز
+ 1) =
= 1 / س(ز + 1)
DoI = FG - FBo = 1 -
ز / (ز + 1) = (ز + 1 - ز)
/ (ز + 1) =
= 1 / (ز + 1).
OI² = 1 / Ø^6(ز + 1)²
+ 1 / (ز + 1)² = (Ø^6 + 1) / Ø^6(ز
+ 1)² =
= 2ز(ز
+ 1) / Ø^6(ز + 1)² =
2 / Ø^4(ز + 1)
OI = (1 / ز) \/¯(2
/ (ز + 1)
It's pretty obvious by now what's going on, lets get one more radial distance just to make sure. We'll find OK next.
In order to find OK we need to know the coordinates of Eo. This is easy
since the
x coordinate of Eo is the same as the point K, which we already know
and is marked on Figure 2, and the same y distance from the origin as the
point Co, which we have already calculated. Eo is at (1 - 1/س,
1 / Ø(ز + 1)).
OK² = OEo² + EoK²
OEo = CoEo - OCo = 1 - 1/س - ز
/ (ز + 1) =
= [س(ز + 1) - (ز + 1) - Ø^5]
/ س(ز + 1)
= س - ز - 1 / س(ز +
1) =
= 1 / Ø^4(ز + 1)
EoK = CoA (calculated above) = 1 / Ø(ز + 1)
OK² = 1 / Ø^8(ز + 1)² + 1 / ز(ز
+ 1)² = (Ø^6 + 1) / Ø^8(ز +
1)² =
= 2ز(ز
+ 1) / Ø^8(ز + 1)² =
2 / Ø^6(ز + 1)
OK = (1 / س) \/¯(2 / (ز
+ 1).
It looks like r, the radial distance of the spiral, increases
or decreases by Ø for every calculation we have made. It only remains
to figure out how large the angle is for each increase in r. It LOOKS like
this angle will be 90°. If we can show that HK and AI are perpendicular,
then we will know that every 90°, r grows or shrinks by Ø.
In order to show that AI and HK are perpendicular, we only have to
show that
angle AOK = 90°.
If <AOK = 90°, then AO² + OK² should = AK², by
the Pythagorean Theorem.
We have already calculated these three distances, so let's just plug
them in:
AO² + OK² = AK² ???
2 / (ز + 1) + 2 / Ø^6(ز + 1) =
[1 - 1 /س ]² ?
2(Ø^6 + 1) / Ø^6(ز + 1) = [(س
- 1) / س]² ?
4ز(ز + 1) / Ø^6(ز + 1)
= 4ز/ Ø^6 ?
; note: (س + 1)² reduces to 4ز
4 / Ø^4 = 4 / Ø^4 _/
Because HK and AI are perpendicular, the angles AOH, HOI, and IOK are
90°.
Every 90° of rotation, the radial distance shrinks or grows by
a factor of Ø.
In order to express this mathematically, we write
r = Ø^-[(2/Pi)t], where t is in radians.
When the spiral is expanding, t is negative, when it is shrinking,
t is positive.
To convert degrees to radians, multiply degrees by Pi / 180.
There is something important to notice here. We have drawn a left-handed
Phi spiral, which necessitates the negative sign on the exponent.
A right-handed spiral could be drawn by placing the line BC to
the left of the line AB in the original triangle from which the drawing
was made (see Constructing
the Phi Spiral ).
In a right-handed spiral, the equation is :
r = Ø^[(2/Pi)t], where t is in radians.
Special characters:
\/¯ ° ¹ ² ³ × ½ ¼
Ø \/¯(ز + 1)