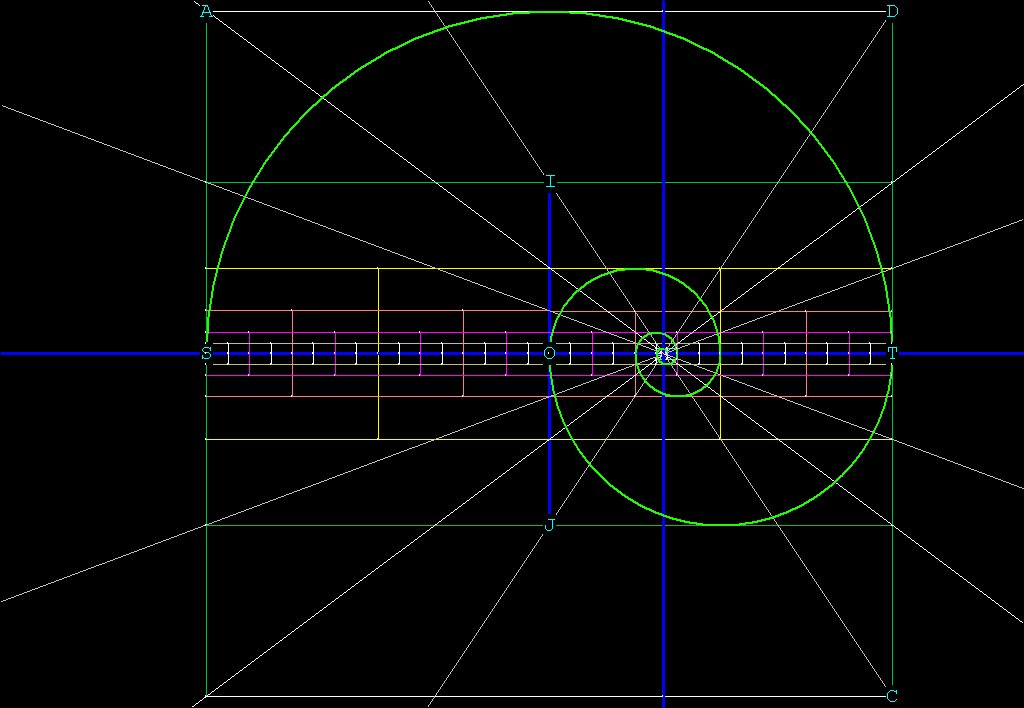
The center of the binary spiral is 1/3 of the way from O to T.
I mentioned that the binary circle pattern has dimension = 2 and that
it is not a fractal. This can be seen by observing that under magnification,
the number of circles increases by 2^magnification power. This is constant
no matter how deeply one goes into the pattern. 2 dimensional fractal patterns
have dimension greater than 2 and less than 3.
In trying to pin down the properties of the binary spiral, I proceeded
in an intuitive fashion. Below is the evolution of my reasoning. I am not
a mathematician, but I get there eventually.
This paper is a good example of how, if you approach a problem with
the idea that it is hard and complex, you will figure out a hard and complex
solution!
There is a simple solution to this problem which I will show at the
end.
Firstly, I noticed how, from O, the radius of the eventual spiral oscillated
back and forth. It looked like it had to converge somewhere.
I noticed that the values for the length of the radius, went from -1
at A to +1 at C, then to 0, etc and generated the following series:
-1, 1, 0, 1/2, 1/4, 3/8, 5/16, 11/32...
Letting p(0) = -1, and p(1) = 1,
I eventually wrote the series out like this:
infinity
E p(k) = p(k-1) +
{ [ |p(k-1) - p(k-2)| * (-1)^k-1 ] / 2 }
k = 2
If you let k = 2, you get 1 + [ 1 - (-1) * -1] / 2
= 0, so p(2) = 0.
When k = 3, you get 0 + [ |0 - 1| ] / 2
= 1/2, so p(3) = 1/2.
etc.
Then I recognized that |p(k-1) - p(k-2)| / 2
= 1 / 2^k,
so the series could be written out as
infinity
E p(k) = p(k-1) +
[ 1 / 2^k * (-1)^k-1 ]
k = 2
This is what is called an alternate infinite series. I'm not very good with infinite series, so I made a table of values:
k | p
-----------
0 | -1
1 | 1
2 | 1 - 1 = 0
3 | 0 + 1/2 =
1/2
4 | 1/2 - 1/4
= 1/4
5 | 1/4 + 1/8
= 3/8
6 | 3/8 - 1/16
= 5/16
7 | 5/16 + 1/32
= 11/32
8 | 11/32 - 1/64 =
21/64
9 | 21/64 + 1/128 =
43/128
10 | 43/128 - 1/256 = 85/256 ......
Even I was able to see from this, for every term after the third, the
numerator for the following term is just the denominator - numerator of
the previous term.
So for 1/2, 2 - 1 = 1, the numerator for the next term, 1/4.
For 1/4, 4 - 1 = 3, the numerator for the next term, 3/8. etc.
and then finally, that for all terms after the third, that for
each alternating term in the series,
3 * numerator + 1 = denominator , then
3 * numerator - 1 = denominator.
For example , for 1/2, 3 * 1 - 1 = 2, which is the denominator
for 1/2.
For 1/4, 3 * 1 + 1 = 4, the denominator for 1/4.
For 3/8, 3 * 3 - 1 = 8, the denominator for 3/8. etc.
I then noticed that each term in the series could be written out as
either
(k + 1) / 3k or (k - 1) / 3k. This is basically 1/3, because
if we divide numerator and denominator by k we get:
(1 +- 1/k) / 3. As k goes to infinity, 1/k
approaches 0 and the limit of the whole thing approaches 1/3.
Of course, if I had just examined a few terms in the first place, I
could have immediately divided the fractions and found each term got closer
and closer to 1/3.
I should have seen this right off the bat! But I approached the problem
thinking there would be difficulty, and so there was.
So what have we learned?
That the oscillating nature of the spiral will converge around the
point 1/3 on the line AC. So the center of the spiral will have coordinates
(1/3, 0).

The center of the binary spiral is 1/3 of the way from O to T.
To find the center geometrically we can find the intersection of any
2 lines that go through the point around which the spiral converges. Lets
find the intersection of the lines IC and DJ. The center of the coordinate
system is at O, which will be (0,0).
CD = ST = 1.
I = (0, 1/4), J = (0, -1/4), D = (1/2, -1/2), C = (1/2, -1/2).
We want to find Z, the center of the spiral.
The equation of line IC is y - 1/4 = -3/4 (x - 0), y = -3/4x
+ 1/4 .
The equation of line DJ is y + 1/4 = 3/4 (x - 0), y = 3/4x
- 1/4 .
The x coordinate of the intersection of the two lines is:
-3/4x + 1/4 = 3/4x - 1/4, 3/2x = 1/2, x = 1/3.
y = 3/4(1/3) - 1/4 = 1/4 - 1/4 = 0.
So geometrically we find the center of the spiral at (1/3, 0) which
is a match to the convergence point we found using the infinite series
above.
From Figure 2, we can see that for every Pi radian rotation of the binary
spiral, r, the distance from the center of the spiral to any point on the
curve, increases or decreases by 2:
From S to the center of the spiral is 1 + 1/3 = 4/3. At T, having revolved
180 degrees, r = 2/3. At O, having revolved a further 180 degrees, r =
1/3, and so on.
Therefore the equation for the binary spiral which is decreasing in
radius, relative to the center of the binary spiral, is:
r = (4/3) * 2^-(t/Pi); t in radians
(We need the 4/3 at the beginning to make r turn out correctly).
For the spiral which is increasing, the equation is
r = (4/3) * 2^(t/Pi); t in radians.